
【题目】在正方体的![]() 个顶点,
个顶点,![]() 个侧面(底面)的中心及体的中心共
个侧面(底面)的中心及体的中心共![]() 个点中,若由两两不同的且不共线的
个点中,若由两两不同的且不共线的![]() 个点构成的平面与由另外
个点构成的平面与由另外![]() 个不同点构成的直线垂直,则称这
个不同点构成的直线垂直,则称这![]() 个点为“正交
个点为“正交![]() 点组”,那么,由这
点组”,那么,由这![]() 个点形成的正交
个点形成的正交![]() 点组的总个数为( )
点组的总个数为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】D
【解析】

如图,设![]() 为体的中心,
为体的中心,![]() 为各侧面中心.
为各侧面中心.
按构成平面的那![]() 个点所在的平面(简称为“
个点所在的平面(简称为“![]() 点平面”)进行分类讨论.
点平面”)进行分类讨论.
观察知![]() 点平面只有
点平面只有![]() 种可能:侧面(如
种可能:侧面(如![]() ),对角面(如
),对角面(如![]() ),由三个顶点构成的正三角形(如
),由三个顶点构成的正三角形(如![]() ),中心面(如
),中心面(如![]() ).
).
(1)当侧面为![]() 时,由
时,由![]() 可构成
可构成![]() 个不共线的
个不共线的![]() 点组(
点组(![]() 点平面,以下同),由
点平面,以下同),由![]() 可构成
可构成![]() 个
个![]() 点组,于是,由
点组,于是,由![]() 点组与
点组与![]() 点组可组合成
点组可组合成![]() 个正交
个正交![]() 点组.另外,由点
点组.另外,由点![]() 及
及![]() 中的某两个点可形成
中的某两个点可形成![]() 个不共线的
个不共线的![]() 点组,任取此
点组,任取此![]() 个
个![]() 点组中的任何一个,例如
点组中的任何一个,例如![]() ,与此
,与此![]() 点组垂直的
点组垂直的![]() 点组为
点组为![]() ,
,![]() ,
,![]() ,故可形成
,故可形成![]() 个正交
个正交![]() 点组.注意到,共有
点组.注意到,共有![]() 个侧面.从而,
个侧面.从而,![]() 点组由侧面形成的正交
点组由侧面形成的正交![]() 点组一共有
点组一共有![]() 个.
个.
(2)当对角面为![]() 时,可知
时,可知![]() 点组由
点组由![]() 中的
中的![]() 个点形成的正交
个点形成的正交![]() 点组共有
点组共有![]() 个.因为一共有
个.因为一共有![]() 个对角面,所以,一共形成
个对角面,所以,一共形成![]() 个该种类型的正交
个该种类型的正交![]() 点组.
点组.
(3)当正三角形为![]() 时,
时,![]() 点组由
点组由![]() 形成,
形成,![]() 点组由
点组由![]() 形成,所以,共有
形成,所以,共有![]() 个正交
个正交![]() 点组.
点组.
(4)当中心面为![]() 时,
时,![]() 点组由
点组由![]() 形成,共有
形成,共有![]() 个正交
个正交![]() 点组.因为共有
点组.因为共有![]() 个中心面,所以,一共有
个中心面,所以,一共有![]() 个该种类型的正交
个该种类型的正交![]() 点组.
点组.
综上所述,一共有![]() 个正交
个正交![]() 点组. 选D.
点组. 选D.


 王后雄学案教材完全解读系列答案
王后雄学案教材完全解读系列答案 海淀课时新作业金榜卷系列答案
海淀课时新作业金榜卷系列答案科目:高中数学 来源: 题型:
【题目】某班级![]() 四位学生
四位学生![]() 参加了文科综合知识竞赛,在竞赛结果公布前,地理老师预测得冠军的是
参加了文科综合知识竞赛,在竞赛结果公布前,地理老师预测得冠军的是![]() 或
或![]() ;历史老师预测得冠军的是
;历史老师预测得冠军的是![]() ;政治老师预测得冠军的不可能是
;政治老师预测得冠军的不可能是![]() 或
或![]() ;语文老师预测得冠军的是
;语文老师预测得冠军的是![]() ,而班主任老师看了竞赛结果后说以上只有两位老师都说对了,则得冠军的是_____。
,而班主任老师看了竞赛结果后说以上只有两位老师都说对了,则得冠军的是_____。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】计算机考试分理论考试与实际操作两部分,每部分考试成绩只记“合格”与“不合格”,两部分考试都“合格”者,则计算机考试“合格”,并颁发合格证书甲、乙、丙三人在理论考试中“合格”的概率依次为![]() ,
,![]() ,
,![]() ,在实际操作考试中“合格”的概率依次为
,在实际操作考试中“合格”的概率依次为![]() ,
,![]() ,
,![]() ,所有考试是否合格相互之间没有影响.
,所有考试是否合格相互之间没有影响.
(1)假设甲、乙、丙三人同时进行理论与实际操作两项考试,谁获得合格证书的可能性最大?
(2)这三人进行理论与实际操作两项考试后,求恰有两人获得合格证书的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】以直角坐标系![]() 的原点为极坐标系的极点,
的原点为极坐标系的极点,![]() 轴的正半轴为极轴.已知曲线
轴的正半轴为极轴.已知曲线![]() 的极坐标方程为
的极坐标方程为![]() ,
,![]() 是
是![]() 上一动点,
上一动点,![]() ,点
,点![]() 的轨迹为
的轨迹为![]() .
.
(1)求曲线![]() 的极坐标方程,并化为直角坐标方程;
的极坐标方程,并化为直角坐标方程;
(2)若点![]() ,直线
,直线![]() 的参数方程
的参数方程![]() (
(![]() 为参数),直线
为参数),直线![]() 与曲线
与曲线![]() 的交点为
的交点为![]() ,当
,当![]() 取最小值时,求直线
取最小值时,求直线![]() 的普通方程.
的普通方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,有三种类型的纸片(可翻转)。
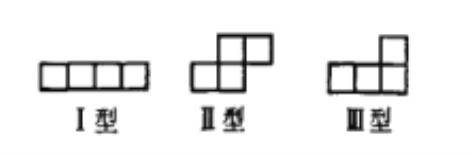
证明:(1)当![]() 时,
时,![]() 的纸板不能分割成若干个I型、II型的纸片;
的纸板不能分割成若干个I型、II型的纸片;
(2)当n为大于2的偶数时,![]() 的纸板可以分割成若干个II型、III型的纸片。
的纸板可以分割成若干个II型、III型的纸片。
查看答案和解析>>
科目:高中数学 来源: 题型:
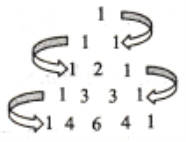
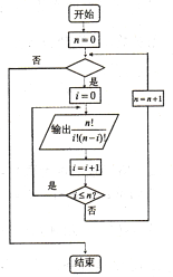
【题目】杨辉三角是二项式系数在三角形中的一种几何排列,是中国古代数学的杰出研究成果之一.在欧洲,左下图叫帕斯卡三角形,帕斯卡在1654年发现的这一规律,比杨辉要迟393年,比贾宪迟600年.某大学生要设计一个程序框图,按右下图标注的顺序将表上的数字输出,若第5次输出数“1”后结束程序,则空白判断框内应填入的条件为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com