【题目】如图，
的三条垂线
、
、
交于点
，
是内的任意一点.求证：
、
、
的外心
、
、
三点共线.
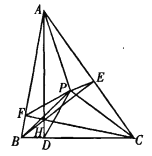
【答案】见解析
【解析】
证法1 如图，过点
作直线
、
、
，与
的三边
、
、
所在的直线分别交于点
、
、
，联结
、
、
.则易知这三条线段的中点分别是
、
、
的外心
、
、
.
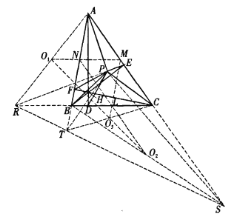
首先证明：、、三点共线.
利用以下性质：若平面上一个角的两边与另一角的两边对应垂直，则这两个角相等或互补.
故
，
，
.
则
.
根据梅涅劳斯定理的逆定理知，、、三点共线.
接下来证明：、、三点共线.
作出的三边、、的中点，分别记为
、
、
.易知、、和、、和、、分别三点共线.则
，
，
.
故
.
根据梅涅劳斯定理的逆定理知，、、三点共线.
证法2 点
对的外接圆的幂为
，对的外接圆的幂为
，对的外接圆的幂为
.由
，
，知
、
、
、
四点共圆.则
.
同理，
，即点对三个圆的幂相同.
又显然点也对三个圆的幂相同，于是，直线
是三个圆中任意两个圆的根轴（公共弦所在的直线）.
因此，、、的外接圆除点外还有一个公共点
，且
通过点.
由连心线垂直平分公共弦知，、、三点均在线段的垂直平分线上.
科目：高中数学 来源： 题型：
【题目】已知二次函数f（x）满足f（x）=f（2-x），且f（1）=6，f（3）=2．
（1）求f（x）的解析式
（2）是否存在实数m，使得在[-1，3]上f（x）的图象恒在直线y=2mx+1的上方？若存在，求m的取值范围；若不存在，说明理由．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】在正方体的
个顶点，
个侧面（底面）的中心及体的中心共
个点中，若由两两不同的且不共线的
个点构成的平面与由另外
个不同点构成的直线垂直，则称这
个点为“正交点组”，那么，由这个点形成的正交点组的总个数为（ ）
A. 
B. 
C. 
D. 
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】下列说法中，正确的命题是（ ）
A.已知随机变量
服从正态分布
，
，则
B.由独立性检验可知，有99%的把握认为物理成绩与数学成绩有关，某人数学成绩优秀，则他有99%的可能物理优秀
C.以模型
去拟合一组数据时，为了求出回归方程，设
，将其变换后得到线性方程
，则c，k的值分别是
和0.3
D.在回归分析模型中，残差平方和越大，说明模型的拟合效果越差
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】某地区2020年清明节前后3天每天下雨的概率为70%，通过模拟实验的方法来计算该地区这3天中恰好有2天下雨的概率：用随机数
（
，且
）表示是否下雨：当
时表示该地区下雨，当
时，表示该地区不下雨，从随机数表中随机取得20组数如下：
332 714 740 945 593 468 491 272 073 445
992 772 951 431 169 332 435 027 898 719
（1）求出
的值，并根据上述数表求出该地区清明节前后3天中恰好有2天下雨的概率；
（2）从2011年开始到2019年该地区清明节当天降雨量（单位：
）如下表：（其中降雨量为0表示没有下雨）.
时间 | 2011年 | 2012年 | 2013年 | 2014年 | 2015年 | 2016年 | 2017年 | 2018年 | 2019年 |
年份 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
降雨量 | 29 | 28 | 26 | 27 | 25 | 23 | 24 | 22 | 21 |
经研究表明：从2011年开始至2020年， 该地区清明节有降雨的年份的降雨量
与年份
成线性回归，求回归直线
，并计算如果该地区2020年（
）清明节有降雨的话，降雨量为多少？（精确到0.01）
参考公式：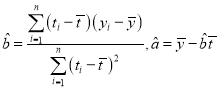
.
参考数据：
，
，
，
.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】为推动乒乓球运动的发展，某乒乓球比赛允许不同协会的运动员组队参加.现有来自甲协会的运动员3名，其中种子选手2名；乙协会的运动员5名，其中种子选手3名.从这8名运动员中随机选择4人参加比赛.
（1）设A为事件“选出的4人中恰有2名种子选手，且这2名种子选手来自同一个协会”，求事件
发生的概率；
（2）设
为选出的4人中种子选手的人数，求随机变量的分布列.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
