
分析 (Ⅰ)由题意和周期公式求出函数周期、ω的值,由正弦函数的性质求出f(x)的对称轴,由对称轴方程求出φ的值,把($\frac{π}{6}$,$\sqrt{3}$)代入求出A,即可得到函数f(x)的解析式;
(Ⅱ)由(Ⅰ)和两角和差的正弦公式化简g(x),由x的范围和正弦函数的性质求出g(x)的最大值和最小值.
解答 解:(Ⅰ)由题意得函数f(x)的周期T=$\frac{7π}{6}-\frac{π}{6}=π$,
所以$\frac{2π}{ω}=π$,得ω=2,…(2分)
易知x=$\frac{\frac{π}{6}+π}{2}$=$\frac{7π}{12}$是f(x)图象的一条对称轴,
所以$2×\frac{7π}{12}+φ=\frac{π}{2}+kπ(k∈Z)$,则$φ=-\frac{2π}{3}+kπ(k∈Z)$,…(4分)
因为0<φ<$\frac{π}{2}$,所以φ=$\frac{π}{3}$,则f(x)=A$sin(2x+\frac{π}{3})$,
因为f(x)过($\frac{π}{6}$,$\sqrt{3}$),所以A$sin(2×\frac{π}{6}+\frac{π}{3})$=$\sqrt{3}$,得A=2,…(6分)
所以函数f(x)=$2sin(2x+\frac{π}{3})$.…(7分)
(Ⅱ)由(I)得,g(x)=[f(x)]2+[f(x+$\frac{π}{3}$)]2
=$4si{n}^{2}(2x+\frac{π}{3})+2si{n}^{2}(2x+π)$=2[1-cos(4x+$\frac{2π}{3}$)+1-cos4x]
=2[2+$\frac{\sqrt{3}}{2}sin4x-\frac{1}{2}cos4x$]=$4+2sin(4x-\frac{π}{6})$ …(10分)
因为$0≤x≤\frac{π}{3}$,所以$-\frac{π}{6}≤4x-\frac{π}{6}≤\frac{7π}{6}$,则$-\frac{1}{2}≤sin(4x-\frac{π}{6})≤1$,…(12分)
所以当$sin(4x-\frac{π}{6})=1$,g(x)max=6,
当$sin(4x-\frac{π}{6})=-\frac{1}{2}$时,g(x)min=3.…(14分)
点评 本题考查函数y=Asin(ωx+φ)的图象解析式的确定,两角和差的正弦公式,以及正弦函数的性质,考查化简、变形能力,属于中档题.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:解答题
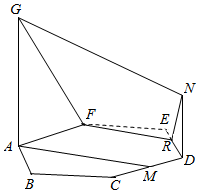 如图,已知ABCDEF是正六边形,GA、ND都垂直于平面ABCDEF,平面FGN交线段DE于点R,点M是CD的中点,AB=DN=1,AG=2.
如图,已知ABCDEF是正六边形,GA、ND都垂直于平面ABCDEF,平面FGN交线段DE于点R,点M是CD的中点,AB=DN=1,AG=2.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 大前提错误 | B. | 小前提错误 | C. | 推理形式错误 | D. | 结论正确 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com