
| A�� | 1 | B�� | 2 | C�� | 3 | D�� | 4 |
���� ���ûع鷽�̡����в�����ָ�������弴���жϳ����������
��� �⣺���ڢ٣����������ݵõ��Ļع鷽��$\stackrel{��}{y}$=$\stackrel{��}{b}$x+$\stackrel{��}{a}$�ع�����������ģ�${\overline x$��$\overline y}$����������ȷ��
���ڢڣ������ָ��R2���̻��ع�Ч����R2��ֵԽ��˵��ģ�͵����Ч��Խ�ã�ԭ�������
���ڢۣ������Իع鷽��$\hat y$=3-2.5x�У�����xÿ����1����λʱ��yƽ������2.5����λ��������ȷ��
���ڢܣ��ڲв�ͼ�У��в��ֲ��Ĵ�״����Ŀ���Խխ��˵��ģ�͵���Ͼ���Խ�ߣ��в�ƽ����ҲԽС��������ȷ��
�����ĸ������У���ȷ����ĸ���Ϊ3��
��ѡ��C��
���� ���⿼���˻ع鷽�̡����в�����ָ����������Ӧ�����⣬�ǻ�����Ŀ��


 ��Կ���Ծ�ϵ�д�
��Կ���Ծ�ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 2 | B�� | -2 | C�� | $\frac{1}{2}$ | D�� | -$\frac{1}{2}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
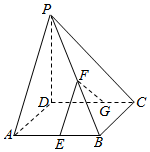 ��ͼ��������P-ABCD�У�PD�͵���ABCD���ҵ���ABCDΪ�����Σ�PD=DC=2��E��F��G�ֱ���AB��PB��CD���е㣮
��ͼ��������P-ABCD�У�PD�͵���ABCD���ҵ���ABCDΪ�����Σ�PD=DC=2��E��F��G�ֱ���AB��PB��CD���е㣮�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com