
设函数f(x)=a2ln x-x2+ax,a>0.
(1)求f(x)的单调区间;
(2)求所有的实数a,使e-1≤f(x)≤e2对x∈[1,e]恒成立.
注:e为自然对数的底数.
 习题精选系列答案
习题精选系列答案科目:高中数学 来源: 题型:
已知双曲线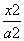 -
- =1(a>0,b>0)的左、右焦点分别为F1、F2,以|F1F2|为直径的圆与双曲
=1(a>0,b>0)的左、右焦点分别为F1、F2,以|F1F2|为直径的圆与双曲 线渐近线的一个交点为(3,4),则此双曲线的方程为( )
线渐近线的一个交点为(3,4),则此双曲线的方程为( )
A.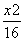 -
- =1 B.
=1 B.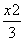 -
-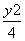 =1
=1
C.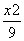 -
-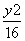 =1 D.
=1 D.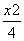 -
-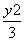 =1
=1
查看答案和解析>>
科目:高中数学 来源: 题型:
设F1,F2是双曲线C: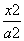 -
-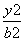 =1(a>0,b>0)的两个焦点,P是C上一点,若|PF1|+|PF2|=6a,且△PF1F2的最小内角为30°,则双曲线C的离心率为________.
=1(a>0,b>0)的两个焦点,P是C上一点,若|PF1|+|PF2|=6a,且△PF1F2的最小内角为30°,则双曲线C的离心率为________.
查看答案和解析>>
科目:高中数学 来源: 题型:
已知函数f(x)=ln x-ax+1在x=2处的切线斜率为-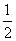 .
.
(1)求实数a的值及函数f(x)的单调区间;
(2)设g(x)=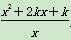 ,对∀x1∈(0,+∞),∃x2∈(-∞,0)使得f(x1)≤g(x2)成立,求正实数k的取值范围;
,对∀x1∈(0,+∞),∃x2∈(-∞,0)使得f(x1)≤g(x2)成立,求正实数k的取值范围;
(3)证明: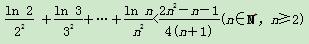 .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
已知集合A={x|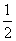 <2x<8,x∈R},B={x|-1<x<m+1,x∈R},若x∈B成立的一个充分不必要的条件是x∈A,则实数m的取值范围是________.
<2x<8,x∈R},B={x|-1<x<m+1,x∈R},若x∈B成立的一个充分不必要的条件是x∈A,则实数m的取值范围是________.
查看答案和解析>>
科目:高中数学 来源: 题型:
设函数f(x)=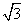 cos(2x+φ)+sin(2x+φ)
cos(2x+φ)+sin(2x+φ)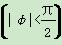 ,且其图象关于直线x=0对称,则( )
,且其图象关于直线x=0对称,则( )
A.y=f(x)的最小正周期为π,且在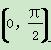 上为增函数
上为增函数
B.y=f(x)的最小正周期为π,且在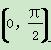 上为减函数
上为减函数
C.y=f(x)的最小正周期为 上为增函数
上为增函数
D.y=f(x)的最小正周期为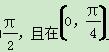 上为减函数
上为减函数
查看答案和解析>>
科目:高中数学 来源: 题型:
已知向量a=(cos ωx,sin ωx),b=(cos ωx,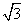 cos ωx),其中0<ω<2.函数f(x)=a·b-
cos ωx),其中0<ω<2.函数f(x)=a·b-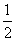 ,其图象的一条对称轴为x=
,其图象的一条对称轴为x= .
.
(1)求函数f(x)的表达式及单调递增区间;
(2)在△ABC中,a,b,c分别为角A,B,C的对边,S为其面积,若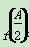 =1,b=1,S△ABC=
=1,b=1,S△ABC=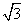 ,求a的值.
,求a的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com