
已知双曲线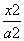 -
- =1(a>0,b>0)的左、右焦点分别为F1、F2,以|F1F2|为直径的圆与双曲
=1(a>0,b>0)的左、右焦点分别为F1、F2,以|F1F2|为直径的圆与双曲 线渐近线的一个交点为(3,4),则此双曲线的方程为( )
线渐近线的一个交点为(3,4),则此双曲线的方程为( )
A.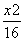 -
- =1 B.
=1 B.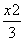 -
-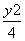 =1
=1
C.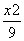 -
-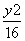 =1 D.
=1 D.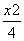 -
-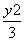 =1
=1
科目:高中数学 来源: 题型:
高三某班有两个数学课外兴趣小组,第一组有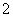 名男生,
名男生,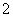 名女生,第二组有
名女生,第二组有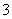 名男生,
名男生,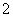 名女生.
名女生. 现在班主任老师要
现在班主任老师要 从第一组选出
从第一组选出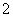 人,从第二组选出
人,从第二组选出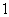 人,请他们在班会上和全班同学分享学习心得.
人,请他们在班会上和全班同学分享学习心得.
(1)求选出的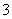 人均是男生的概率;(2)求选出的
人均是男生的概率;(2)求选出的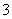 人中有男生也有女生的概率.
人中有男生也有女生的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
已知下列三个命题:①若一个球的半径缩小到原来的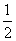 ,则其体积缩小到原来的
,则其体积缩小到原来的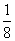 ;②若两组数据的平均数相等,则它们的标准差也相等;③直线x+y+1=0与圆x2+y2=
;②若两组数据的平均数相等,则它们的标准差也相等;③直线x+y+1=0与圆x2+y2=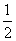 相切.
相切.
其中真命题的序号是( )
A.①②③ B.①② C.①③ D.②③
查看答案和解析>>
科目:高中数学 来源: 题型:
已知函数f(x)=k(x-1)ex+x2.
(1)当k=- 时,求函数f(x)在点(1,1)处的切线方程;
时,求函数f(x)在点(1,1)处的切线方程;
(2)若在y轴的左侧,函数g(x)=x2+(k+2)x的图象恒在f(x)的导函数f′(x)图象的上方,求k的取值范围;
(3)当k≤-1时,求函数f(x)在[k,1]上的最小值m.
查看答案和解析>>
科目:高中数学 来源: 题型:
设函数f(x)=a2ln x-x2+ax,a>0.
(1)求f(x)的单调区间;
(2)求所有的实数a,使e-1≤f(x)≤e2对x∈[1,e]恒成立.
注:e为自然对数的底数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com