
分析 利用正弦定理化简已知的等式,再利用两角和的正弦函数公式及诱导公式化简,根据sinB不为0,得到cosA的值,由A的范围,利用特殊角的三角函数值即可求出A的度数.
解答 解:因为(2b-c)cosA-acosC=0,
由正弦定理可得:(2sinB-sinC)cosA=sinAcosC,
即2sinBcosA=sinCcosA+cosCsinA=sin(A+C)=sinB,
由B∈(0,180°),得到sinB≠0,
所以cosA=$\frac{1}{2}$,
又A∈(0,180°),
则A的度数为60°,即在A处望B、C所成的角的大小为60°.
故答案为:60°.
点评 此题考查学生灵活运用正弦定理化简求值,灵活运用两角和的正弦函数公式及诱导公式化简求值,是一道中档题.


 寒假大串联黄山书社系列答案
寒假大串联黄山书社系列答案 寒假创新型自主学习第三学期寒假衔接系列答案
寒假创新型自主学习第三学期寒假衔接系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
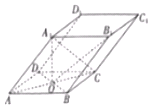 如图,四棱柱ABCD-A1B1C1D1的底面AB是CD菱形,AC∩BD=O,A1O⊥底面ABCD,AB=AA1=2.
如图,四棱柱ABCD-A1B1C1D1的底面AB是CD菱形,AC∩BD=O,A1O⊥底面ABCD,AB=AA1=2.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ①②③ | B. | ①②④ | C. | ①③④ | D. | ①②③④ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | α=-β | B. | α=180°+β | ||
| C. | α=k•360°+β,k∈Z | D. | α=k•360°±180°+β,k∈Z |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com