练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    △ABC中∠C=
    π
    3
    ，AB=2，则△ABC的周长的最大值为
     
    ．
    考点：余弦定理
    专题：解三角形
    分析：由题意可得△ABC的周长=AB+AC+BC=2+
    4
    		3
    sinB+
    4
    		3
    sinA=2+4sin（A+
    π
    6
    ），结合A的范围可得答案．
    解答： 解：由正弦定理可得
    2
    sin
    π
    3
    =
    AC
    sinB
    =
    BC
    sinA
    ，
    ∴可得AC=
    4
    		3
    sinB，BC=
    4
    		3
    sinA，
    ∴△ABC的周长=AB+AC+BC=2+
    4
    		3
    sinB+
    4
    		3
    sinA，
    =2+
    4
    		3
    sin（
    2π
    3
    -A）+
    4
    		3
    sinA
    =2+4sin（A+
    π
    6
    ），
    ∵A∈（0，
    2π
    3
    ），∴A+
    π
    6
    ∈（
    π
    6
    ，
    5π
    6
    ），
    ∴sin（A+
    π
    6
    ）∈（
    1
    2
    ，1]
    ∴当sin（A+
    π
    6
    ）=1时，△ABC的周长2+4sin（A+
    π
    6
    ）取最大值6，
    故答案为：6
    点评：本题考查三角函数的最值，涉及正弦定理的应用，属基础题．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

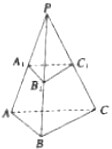    如图所示，已知三棱锥P-ABC中，PA=a，PB=b，PC=c，侧棱PA、PB、PC上各有一点A1，B1、C1，且PA1=a1，PB1=b1，PC1=c1，求证：
    VP-ABC
    VP-A1B1C1
    =
    abc
    a1b1c1
    ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    △ABC的三个内角A，B，C所对的边分别为a，b，c，
    m
    =（-1，1），
    n
    =（cosBcosC，sinBsinC-
    		3
    2
    ）且
    m
    ⊥
    n
    ，求角A的大小．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知函数f（x）=
    2x-1
    2x+1
    ，求f（x）在（-∞，+∞）上是增函数．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知
    OA
    =（a，b），|
    OA
    |=1，求点P（a+b，ab）的轨迹方程．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    对某班级50名学生学习数学与学习物理的成绩进行调查，得到如表所示：
    数学成绩较好数学成绩一般合计
    物理成绩较好18725
    物理成绩一般61925
    合计242650
    由K2=
    n(ad-bc)2
    (a+b)(c+d)(a+c)(b+d)
    ，解得K2=
    50×(18×19-6×7)2
    25×25×24×26
    ≈11.5
    P（K2≥k）0.0500.0100.001
    k3.8416.63510.828
    参照附表，得到的正确结论是（　　）
    A、在犯错误的概率不超过0.1%的前提下，认为“数学成绩与物理成绩有关”
    B、在犯错误的概率不超过0.1%的前提下，认为“数学成绩与物理成绩无关”
    C、有100%的把握认为“数学成绩与物理成绩有关”
    D、有99%以上的把握认为“数学成绩与物理成绩无关”

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    观测两相关变量得如下数据
    x-1-2-3-4-554321
    y-1.1-1.9-2.9-4.1-554.12.91.91.1
    则两变量x，y间的回归直线必过点
     
    ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    为了庆祝2012年元旦，某班团支部决定组织班里48名同学去水上公园坐船观赏风景，支部先派一个人去了解船只的租金情况，看到的租金价格如下表，那么，怎样他们合理设计租船方案后，所付租金最少为
     
    元．
    船型每只限载人数租金（元/只）
    大船512
    小船38

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知k∈R，设f（θ）=cos2θ+（k-4）sinθ+2k-9，其中θ∈[0，2π）．
    （1）当k=3时，求f（θ）的最值，并求相应的θ；
    （2）若对任意θ∈[0，2π），f（θ）≤0恒成立，求k的取值范围；
    （3）若存在唯一的θ∈[0，2π），使f（θ）≤0，求θ、k的取值．

    查看答案和解析>>

    同步练习册答案