Question

12．设偶函数f（x）（x∈R）满足f（x）=f（2-x），且当x∈[0，1]时，f（x）=x²．又函数g（x）=|cos（πx）|，则函数h（x）=g（x）-f（x）在区间$[{-\frac{1}{2}，\frac{3}{2}}]$上的零点个数为（　　）

• A． 5
• B． 6
• C． 7
• D． 8

Answer 1

分析 根据条件可得f（x）是周期函数，T=2，且是偶函数，令h（x）=0，则f（x）=g（x），在同一坐标系中作y=f（x）和y=g（x）在区间$[{-\frac{1}{2}，\frac{3}{2}}]$上的图象，由图象可得结论．

解答 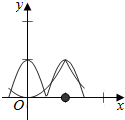解：∵f（x）=f（2-x），故f（x）的图象关于x=1对称，
又函数f（x）是R上的偶函数，∴f（x+2）=f（-x）=f（x），
∴f（x）是周期函数，T=2，
当x∈[-1，0]时，f（x）=f（-x）=x²．
令h（x）=0，则f（x）=g（x），
在同一坐标系中作y=f（x）和y=g（x）在区间$[{-\frac{1}{2}，\frac{3}{2}}]$上的图象，
由图象可得y=f（x）和y=g（x）有5个交点，
故函数h（x）=f（x）-g（x）的零点个数为5．
故选：A．

点评 本题考查函数零点的定义，体现了数形结合的数学思想，在同一坐标系中作y=f（x）和y=g（x）的图象，是解题的关键．