
【题目】已知函数f(x)= ![]() sin2x+sinxcosx﹣
sin2x+sinxcosx﹣ ![]()
(1)求函数y=f(x)在[0, ![]() ]上的单调递增区间;
]上的单调递增区间;
(2)将函数y=f(x)的图象向左平移 ![]() 个单位长度,再将图象上所有点的横坐标伸长到原来的2倍(纵坐标不变),得到函数y=g(x)的图象,求证:存在无穷多个互不相同的整数x0 , 使得g(x0)>
个单位长度,再将图象上所有点的横坐标伸长到原来的2倍(纵坐标不变),得到函数y=g(x)的图象,求证:存在无穷多个互不相同的整数x0 , 使得g(x0)> ![]() .
.
【答案】
(1)解:f(x)= ![]() sin2x+sinxcosx﹣
sin2x+sinxcosx﹣ ![]() =
= ![]() =
= ![]() =sin(2x﹣
=sin(2x﹣ ![]() );
);
因为2kπ≤2x﹣ ![]() ≤2kπ
≤2kπ ![]() ,∴kπ
,∴kπ ![]() ≤x≤kπ
≤x≤kπ ![]() ,k∈Z,
,k∈Z,
所以函数y=f(x)在[0, ![]() ]上的单调递增区间为[0,
]上的单调递增区间为[0, ![]() ]
]
(2)解:将函数向左平移 ![]() 个单位长度,再将图象上所有点的横坐标伸长到原来的2倍(纵坐标不变),得到函数y=g(x)=sinx,g(x0)>
个单位长度,再将图象上所有点的横坐标伸长到原来的2倍(纵坐标不变),得到函数y=g(x)=sinx,g(x0)> ![]() .即sinx>
.即sinx> ![]() ,
,
所以2kπ ![]() <x<2kπ
<x<2kπ ![]() ,k∈Z,
,k∈Z,
则(2kπ ![]() )﹣(2k
)﹣(2k ![]() )=
)= ![]() >1,所以对任意的整数k都存在x0∈(2kπ
>1,所以对任意的整数k都存在x0∈(2kπ ![]() ,2kπ
,2kπ ![]() ),k∈Z,
),k∈Z,
即存在无穷多个互不相同的整数x0,使得g(x0)> ![]()
【解析】(1)化简三角函数式,利用正弦函数的单调性求单调区间;(2)利用三角函数图象的变换规律得到函数y=g(x),然后证明.
【考点精析】解答此题的关键在于理解正弦函数的单调性的相关知识,掌握正弦函数的单调性:在![]()
![]() 上是增函数;在
上是增函数;在![]()
![]() 上是减函数,以及对函数y=Asin(ωx+φ)的图象变换的理解,了解图象上所有点向左(右)平移
上是减函数,以及对函数y=Asin(ωx+φ)的图象变换的理解,了解图象上所有点向左(右)平移![]() 个单位长度,得到函数
个单位长度,得到函数![]() 的图象;再将函数
的图象;再将函数![]() 的图象上所有点的横坐标伸长(缩短)到原来的
的图象上所有点的横坐标伸长(缩短)到原来的![]() 倍(纵坐标不变),得到函数
倍(纵坐标不变),得到函数![]() 的图象;再将函数
的图象;再将函数![]() 的图象上所有点的纵坐标伸长(缩短)到原来的
的图象上所有点的纵坐标伸长(缩短)到原来的![]() 倍(横坐标不变),得到函数
倍(横坐标不变),得到函数![]() 的图象.
的图象.


科目:高中数学 来源: 题型:
【题目】先将函数y=2sinx的图象纵坐标不变,横坐标压缩为原来一半,再将得到的图象向左平移 ![]() 个单位,则所得图象的对称轴可以为( )
个单位,则所得图象的对称轴可以为( )
A.x=﹣ ![]()
B.x= ![]()
C.x=﹣ ![]()
D.x= ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=plnx+(p﹣1)x2+1.
(1)讨论函数f(x)的单调性;
(2)当P=1时,f(x)≤kx恒成立,求实数k的取值范围;
(3)证明:1n(n+1)<1+ ![]() …+
…+ ![]() (n∈N+).
(n∈N+).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,直四棱柱ABCD﹣A1B1C1D1中,AB∥CD,AB⊥AD,AD=AB=1.AA1=CD=2.E为棱DD1的中点. 
(1)证明:B1C1⊥平面BDE;
(2)求二面角D﹣BE﹣C1的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=f'(1)ex﹣1﹣f(0)x+ ![]() 的导数,e为自然对数的底数)g(x)=
的导数,e为自然对数的底数)g(x)= ![]() +ax+b(a∈R,b∈R)
+ax+b(a∈R,b∈R)
(Ⅰ)求f(x)的解析式及极值;
(Ⅱ)若f(x)≥g(x),求 ![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知正方形OABC边长为3,点M,N分别为线段BC,AB上一点,且2BM=MC,AN=NB,P为△BNM内一点(含边界),设 ![]() (λ,μ为实数),则
(λ,μ为实数),则 ![]() 的最大值为
的最大值为 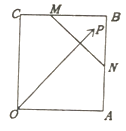
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,我海监船在D岛海域例行维权巡航,某时刻航行至A处,此时测得其北偏东30°方向与它相距20海里的B处有一外国船只,且D岛位于海监船正东18海里处. 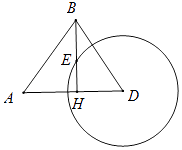
(1)求此时该外国船只与D岛的距离;
(2)观测中发现,此外国船只正以每小时4海里的速度沿正南方航行.为了将该船拦截在离D岛12海里的E处(E在B的正南方向),不让其进入D岛12海里内的海域,试确定海监船的航向,并求其速度的最小值(角度精确到0.1°,速度精确到0.1海里/小时).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com