
(本小题8分) 已知圆 :
:  和圆外一点
和圆外一点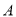 (1,
(1, 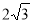 ),
),
(1)若直线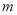 经过原点
经过原点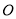 ,且圆
,且圆 上恰有三个点到直线
上恰有三个点到直线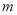 的距离为
的距离为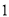 ,求直线
,求直线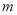 的方程;
的方程;
(2)若经过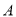 的直线
的直线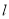 与圆
与圆 相切,切点分别为
相切,切点分别为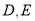 ,求切线
,求切线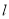 的方程及
的方程及 两切点所在的直线方程.
两切点所在的直线方程.
(1)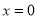 ,(2)
,(2)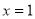 或
或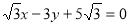 ,(3)
,(3)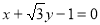 ,
,
【解析】
试题分析:已知圆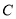 的圆心为
的圆心为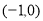 ,半径
,半径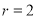 ,要使圆
,要使圆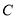 上恰有三个点到直线
上恰有三个点到直线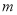 的距离为1,因圆的半径为2,则圆心到直线
的距离为1,因圆的半径为2,则圆心到直线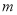 的距离恰为1,所求直线
的距离恰为1,所求直线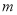 经过原点,满足圆心到直线
经过原点,满足圆心到直线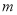 的距离为1,设直线方程后用待定系数法求出即可. 第二步求圆的切线方程,可先设出直线的方程,然后利用相切条件,圆心到直线的距离等于半径,求出斜率
的距离为1,设直线方程后用待定系数法求出即可. 第二步求圆的切线方程,可先设出直线的方程,然后利用相切条件,圆心到直线的距离等于半径,求出斜率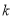 ,再写出切线方程即可;最后利用四点
,再写出切线方程即可;最后利用四点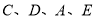 共圆,写出圆的方程,
共圆,写出圆的方程,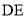 为两圆的公共弦,其方程只需用两圆的方程相减的得到即可.
为两圆的公共弦,其方程只需用两圆的方程相减的得到即可.
试题解析:(1)圆C的圆心为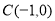 ,半径
,半径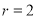 ,圆
,圆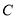 上恰有三个点到直线
上恰有三个点到直线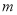 的距离为1,则圆心到直线
的距离为1,则圆心到直线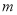 的距离恰为1,当直线的斜率存在时,不妨设直线方程为
的距离恰为1,当直线的斜率存在时,不妨设直线方程为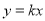 ,设圆心
,设圆心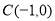 到直线
到直线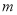 的距离为
的距离为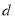 ,由
,由 ,
,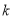 无解,当直线斜率不存在时,直线
无解,当直线斜率不存在时,直线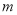 的方程为
的方程为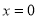 符合题意,所以所求直线为
符合题意,所以所求直线为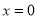 .(2)当直线的斜率存在时,设直线方程为
.(2)当直线的斜率存在时,设直线方程为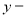
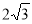
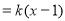 ,即
,即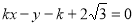 ,设圆心
,设圆心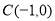 到直线
到直线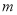 的距离为
的距离为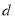 ,则
,则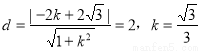 ,所求直线为
,所求直线为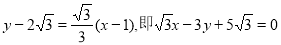 ,当直线的斜率不存在时,直线方程为
,当直线的斜率不存在时,直线方程为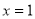 符合题意,则所求的切线方程为
符合题意,则所求的切线方程为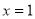 或
或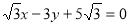 ,由于
,由于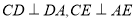 ,则四点
,则四点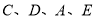 共圆,圆心
共圆,圆心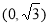 ,半径为4,写出圆的方程
,半径为4,写出圆的方程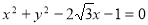 ,而
,而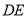 为两圆的公共弦,把两圆的方程相减,得:
为两圆的公共弦,把两圆的方程相减,得: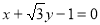
考点:1.直线与圆相交、相切问题;2.求两圆的公共弦方程;


科目:高中数学 来源:2014-2015学年湖北省武汉市武昌区高三元月调研考试理科数学试卷(解析版) 题型:选择题
根据如下样本数据
x | 3 | 4 | 5 | 6 | 7 |
y | 4.0 | 2.5 |
| 0.5 |
|
得到的回归方程为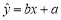 .若
.若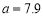 ,则
,则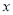 每增加1个单位,
每增加1个单位,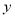 就
就
A.增加 个单位 B.减少
个单位 B.减少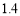 个单位
个单位
C.增加 个单位 D.减少
个单位 D.减少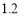 个单位
个单位
查看答案和解析>>
科目:高中数学 来源:2014-2015学年福建省福州市高三上学期期末质量检测理科数学试卷(解析版) 题型:选择题
已知抛掷一枚质地均匀的硬币,正面朝上的概率为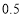 .现采用随机模拟试验的方法估计抛掷这枚硬币三次恰有两次正面朝上的概率:先由计算器产生0或1的随机数,用0表示正面朝上,用1表示反面朝上;再以每三个随机数做为一组,代表这三次投掷的结果.经随机模拟试验产生了如下20组随机数:
.现采用随机模拟试验的方法估计抛掷这枚硬币三次恰有两次正面朝上的概率:先由计算器产生0或1的随机数,用0表示正面朝上,用1表示反面朝上;再以每三个随机数做为一组,代表这三次投掷的结果.经随机模拟试验产生了如下20组随机数:
101 111 010 101 010 100 100 011 111 110
000 011 010 001 111 011 100 000 101 101
据此估计,抛掷这枚硬币三次恰有两次正面朝上的概率为( ).
A.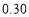 B.
B.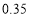 C.
C.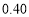 D.
D.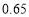
查看答案和解析>>
科目:高中数学 来源:2014-2015学年浙江省高二上学期第二次统练文科数学试卷(解析版) 题型:填空题
如图,在长方形 中,
中,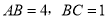
 为
为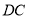 的四等分点(靠近
的四等分点(靠近 处),
处), 为线段
为线段 上一动点(包括端点),现将
上一动点(包括端点),现将 沿
沿 折起,使
折起,使 点在平面内的射影恰好落在边
点在平面内的射影恰好落在边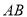 上,则当
上,则当 运动时,二面角
运动时,二面角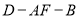 的平面角余弦值的变化范围为 .
的平面角余弦值的变化范围为 .

查看答案和解析>>
科目:高中数学 来源:2014-2015学年浙江省高二上学期第二次统练文科数学试卷(解析版) 题型:选择题
已知点 是椭圆
是椭圆 上的任意一点,
上的任意一点,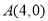 ,若
,若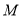 为线段
为线段 中点,则点
中点,则点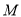 的轨迹方程是 ( )
的轨迹方程是 ( )
A. B.
B.
C.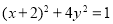 D.
D.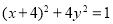
查看答案和解析>>
科目:高中数学 来源:2014-2015学年浙江省高二上学期第二次统练理科数学试卷(解析版) 题型:填空题
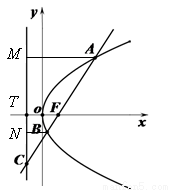
如图,过抛物线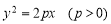 的焦点F的直线
的焦点F的直线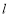 交抛物线于点A、B,交其准线于点C,若
交抛物线于点A、B,交其准线于点C,若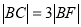 ,且
,且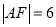 ,则此抛物线的方程为_____________
,则此抛物线的方程为_____________
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com