
【题目】下列命题正确的是( )
A.若数列![]() 、
、![]() 的极限都存在,且
的极限都存在,且![]() ,则数列
,则数列![]() 的极限存在
的极限存在
B.若数列![]() 、
、![]() 的极限都不存在,则数列
的极限都不存在,则数列![]() 的极限也不存在
的极限也不存在
C.若数列![]() 、
、![]() 的极限都存在,则数列
的极限都存在,则数列![]() 、
、![]() 的极限也存在
的极限也存在
D.数![]() ,若数列
,若数列![]() 的极限存在,则数列
的极限存在,则数列![]() 的极限也存在
的极限也存在
科目:高中数学 来源: 题型:
【题目】如图,四棱锥S-ABCD的底面是边长为1的正方形,则棱SB垂直于底面.
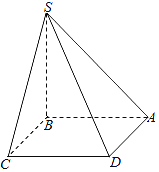
(1)求证:平面SBD⊥平面SAC;
(2)若SA与平面SCD所成角的正弦值为![]() ,求SB的长.
,求SB的长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知p:方程x2+y2﹣4x+m2=0表示圆:q:方程![]() 1(m>0)表示焦点在y轴上的椭圆.
1(m>0)表示焦点在y轴上的椭圆.
(1)若p为真命题,求实数m的取值范围;
(2)若命题p、q有且仅有一个为真,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线![]() 的参数方程为
的参数方程为 (
(![]() 为参数),以坐标原点为极点,
为参数),以坐标原点为极点, ![]() 轴的非负半轴为极轴建立极坐标系,圆
轴的非负半轴为极轴建立极坐标系,圆![]() 的极坐标方程为
的极坐标方程为![]() ,直线
,直线![]() 与圆
与圆![]() 交于
交于![]() ,
, ![]() 两点.
两点.
(1)求圆![]() 的直角坐标方程及弦
的直角坐标方程及弦![]() 的长;
的长;
(2)动点![]() 在圆
在圆![]() 上(不与
上(不与![]() ,
, ![]() 重合),试求
重合),试求![]() 的面积的最大值.
的面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知等差数列![]() 的前
的前![]() 项和为
项和为![]() ,
,![]() ,公差为
,公差为![]() .
.
(1)若![]() ,求数列
,求数列![]() 的通项公式;
的通项公式;
(2)是否存在![]() ,
,![]() 使
使![]() 成立?若存在,试找出所有满足条件的
成立?若存在,试找出所有满足条件的![]() ,
,![]() 的值,并求出数列
的值,并求出数列![]() 的通项公式;若不存在,请说明理由.
的通项公式;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】4个不同的红球和6个不同的白球放入同一个袋中,现从中取出4个球.
(1)若取出的红球的个数不少于白球的个数,则有多少不同的取法?
(2)取出一个红球记2分,取出一个白球记1分,若取出4个球所得总分不少于5分,则有多少种不同取法.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】艾滋病是一种危害性极大的传染病,由感染艾滋病病毒![]() 病毒
病毒![]() 引起,它把人体免疫系统中最重要的CD4T淋巴细胞作为主要攻击目标,使人体丧失免疫功能
引起,它把人体免疫系统中最重要的CD4T淋巴细胞作为主要攻击目标,使人体丧失免疫功能![]() 下表是近八年来我国艾滋病病毒感染人数统计表:
下表是近八年来我国艾滋病病毒感染人数统计表:
年份 | 2011 | 2012 | 2013 | 2014 | 2015 | 2016 | 2017 | 2018 |
年份代码x | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
感染者人数 |
|
|
|
|
|
|
| 85 |
![]() 请根据该统计表,画出这八年我国艾滋病病毒感染人数的折线图;
请根据该统计表,画出这八年我国艾滋病病毒感染人数的折线图;
![]() 请用相关系数说明:能用线性回归模型拟合y与x的关系;
请用相关系数说明:能用线性回归模型拟合y与x的关系;
![]() 建立y关于x的回归方程
建立y关于x的回归方程![]() 系数精确到
系数精确到![]() ,预测2019年我国艾滋病病毒感染人数.
,预测2019年我国艾滋病病毒感染人数.
参考数据:![]() ;
;![]() ,
,![]() ,
,![]() ,
,
参考公式:相关系数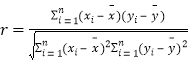 ,
,
回归方程![]() 中,
中,![]()
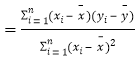 ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
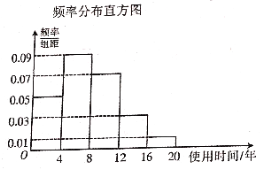
【题目】为了解一款电冰箱的使用时间和市民对这款电冰箱的购买意愿,研究人员对该款电冰箱进行了相应的抽样调查,得到数据的统计图表如下:
购买意愿市民年龄 | 不愿意购买该款电冰箱 | 愿意购买该款电冰箱 | 总计 |
40岁以上 | 600 | 800 | |
40岁以下 | 400 | ||
总计 | 800 |
(1)根据图中的数据,估计该款电冰箱使用时间的中位数;
(2)完善表中数据,并据此判断是否有![]() 的把握认为“愿意购买该款电冰箱“与“市民年龄”有关;
的把握认为“愿意购买该款电冰箱“与“市民年龄”有关;
(3)用频率估计概率,若在该电冰箱的生产线上随机抽取3台,记其中使用时间不低于4年的电冰箱的台数为![]() ,求
,求![]() 的期望.
的期望.
附:![]()
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com