
���� ����������Բ�������ʹ�ʽ���㵽ֱ�ߵľ��빫ʽ���������a��b��ֵ�������ԲC�ķ��̣�
������ֱ��l�ķ��̣�������Բ���̣�����Τ�ﶨ�����ҳ���ʽ���حGHح�����ɵ㵽ֱ�ߵľ��빫ʽ�������ε������ʽ��á�OGH����������1+4k2-2m2=0�������е����깫ʽ��ֱ�ߵ�б�ʹ�ʽ���s��t��ֵ��ʹ��ֱ��PM��PN��б��֮��Ϊ��ֵ����ֵΪ$-\frac{1}{4}$��
��� �⣺����������֪$e=\frac{{\sqrt{3}}}{2}$����${e^2}=\frac{c^2}{a^2}-\frac{{{a^2}-{b^2}}}{a^2}=\frac{3}{4}$����a2=4b2��
����ԭ��ΪԲ�㣬��ԲC�Ķ̰��᳤Ϊ�뾶��ԲΪ��Բx2+y2=b2��
��Բx2+y2=b2��ֱ��$x-y+\sqrt{2}=0$���У���$b=\frac{{\sqrt{2}}}{{\sqrt{{1^2}+{{��{-1}��}^2}}}}=1$��
����a2=4b2=4��
����������ԲC�ķ���Ϊ$\frac{x^2}{4}+y=1$��
������ֱ��l��y=kx+m��m��0����G��x1��y1����H��x2��y2����
����$\left\{\begin{array}{l}{y=kx+m}\\{\frac{{x}^{2}}{4}+{y}^{2}=1}\end{array}\right.$���ã�1+4k2��x2+8kmx+4m2-4=0��
��$��={��{8km}��^2}-4��{1+4{k^2}}����{4{m^2}-4}��=16��{4{k^2}+1-{m^2}}����0��{x_1}+{x_2}=-\frac{8km}{{1+4{k^2}}}��{x_1}{x_2}=\frac{{4{m^2}-4}}{{1+4{k^2}}}$��
�����ҳ���ʽ֪حGHح=$\sqrt{1+{k}^{2}}$•$\sqrt{��{x}_{1}+{x}_{2}��^{2}-4{x}_{1}{x}_{2}}$=$\frac{\sqrt{1+{k}^{2}}•\sqrt{4{k}^{2}+1-{m}^{2}}}{1+4{k}^{2}}$
�ָ��ݵ㵽ֱ�ߵľ��빫ʽ֪ԭ��O��ֱ��y=kx+m�ľ���Ϊ$d=\frac{|m|}{{\sqrt{1+4{k^2}}}}$��
���ǡ�OGH�����Ϊ$S=\frac{1}{2}•|{GH}|•\frac{|m|}{{\sqrt{1+4{k^2}}}}=\frac{{2|m|•\sqrt{4{k^2}+1-{m^2}}}}{{1+4{k^2}}}=1$��
�����ã�1+4k2-2m2��2=0������1+4k2-2m2=0����
���߶�GH���е�$P��{-\frac{4km}{{1+4{k^2}}}��\frac{m}{{1+4{k^2}}}}��$����$P��{-\frac{2k}{m}��\frac{1}{2m}}��$��
����������������Ķ���M��N��������M��s��0����N��-s��0����s��0����
ֱ��PM��PN��б��֮��Ϊt��
����$t={k_{PM}}•{k_{PN}}=\frac{{\frac{1}{2m}}}{{-\frac{2k}{3}-s}}��\frac{{\frac{1}{2m}}}{{-\frac{2k}{m}+s}}$=$\frac{1}{{4��{4{k^2}-{s^2}{m^2}}��}}$��
���$\left\{\begin{array}{l}{s=\sqrt{2}}\\{t=-\frac{1}{4}}\end{array}\right.$��
�����������$M��{-\sqrt{2}��0}����N��{\sqrt{2}��0}��$��ʹ��ֱ��PM��PN��б��֮��Ϊ��ֵ����ֵΪ$-\frac{1}{4}$��
���� ���⿼����Բ�ı����̼��������ʣ�ֱ������Բ��λ�ù�ϵ������Τ�ﶨ�����ҳ���ʽ��ֱ�ߵ�б�ʹ�ʽ���ۺ�Ӧ�ã�������������������е��⣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | -1 | B�� | 1 | C�� | $\frac{10}{3}$ | D�� | $\frac{11}{2}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
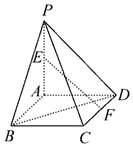 ��ͼ��ƽ��PAD��ƽ��ABCD���ı���ABCDΪ�����Σ���PAD=90�㣬��PA=AD=2��E��F�ֱ����߶�PA��CD���е㣬������ֱ��EF��BD���ɽǵ�����ֵΪ$\frac{\sqrt{3}}{6}$��
��ͼ��ƽ��PAD��ƽ��ABCD���ı���ABCDΪ�����Σ���PAD=90�㣬��PA=AD=2��E��F�ֱ����߶�PA��CD���е㣬������ֱ��EF��BD���ɽǵ�����ֵΪ$\frac{\sqrt{3}}{6}$���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{1}{4}$ | B�� | $\frac{1}{3}$ | C�� | $\frac{1}{2}$ | D�� | 1 |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com