Question

13．在平面内，定点A，B，C，D满足|$\overrightarrow{DA}$|=|$\overrightarrow{DB}$|=|$\overrightarrow{DC}$|，|$\overrightarrow{DA}$|•|$\overrightarrow{DB}$|=|$\overrightarrow{DB}$|•|$\overrightarrow{DC}$|=|$\overrightarrow{DC}$|•|$\overrightarrow{DA}$|=-4，动点P，M满足|$\overrightarrow{AP}$|=2，$\overrightarrow{PM}$=$\overrightarrow{MC}$，则|$\overrightarrow{BM}$|的最大值是3$\sqrt{2}$+1．

Answer 1

分析 根据条件可知A，B，C三点共圆，M为PC的中点，于是$\overrightarrow{BM}$=$\frac{1}{2}$（$\overrightarrow{BP}+\overrightarrow{BC}$）．建立平面直角坐标系得出$\overrightarrow{BC}，\overrightarrow{BP}$的坐标，计算${\overrightarrow{BM}}^{2}$得出模长关于α的函数，利用三角函数的恒等变换得出模长的最大值．

解答 解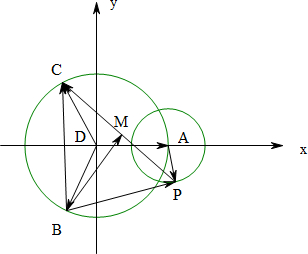：∵|$\overrightarrow{DA}$|=|$\overrightarrow{DB}$|=|$\overrightarrow{DC}$|，∴A，B，C在以D为圆心的圆D上，
∵$\overrightarrow{DA}$•$\overrightarrow{DB}$=$\overrightarrow{DB}$$•\overrightarrow{DC}$=$\overrightarrow{DC}$•$\overrightarrow{DA}$=-4，∴$\overrightarrow{DA}，\overrightarrow{DB}，\overrightarrow{DC}$两两夹角相等均为120°，∴|DA|=2$\sqrt{2}$，
以D为原点建立平面直角坐标系，设A（2$\sqrt{2}$，0），则B（-$\sqrt{2}$，-$\sqrt{6}$），C（-$\sqrt{2}$，$\sqrt{6}$），
∴$\overrightarrow{BC}$=（0，2$\sqrt{6}$）．
∵|$\overrightarrow{AP}$|=2，∴P在以A为圆心，以2为半径的圆A上，
∵$\overrightarrow{PM}$=$\overrightarrow{MC}$，∴M为PC的中点，∴$\overrightarrow{BM}$=$\frac{1}{2}$（$\overrightarrow{BP}+\overrightarrow{BC}$）．
设P（2$\sqrt{2}$+2cosα，2sinα），则$\overrightarrow{BP}$=（3$\sqrt{2}$+2cosα，2sinα+$\sqrt{6}$），
∴$\overrightarrow{BM}$=$\frac{1}{2}$（$\overrightarrow{BP}+\overrightarrow{BC}$）=（cosα+$\frac{3\sqrt{2}}{2}$，sinα+$\frac{3\sqrt{6}}{2}$），
∴${\overrightarrow{BM}}^{2}$=（cosα+$\frac{3\sqrt{2}}{2}$）²+（sinα+$\frac{3\sqrt{6}}{2}$）²=3$\sqrt{2}$cosα+3$\sqrt{6}$sinα+19=6$\sqrt{2}$sin（α+$\frac{π}{6}$）+19，
∴|$\overrightarrow{BM}$|的最大值为$\sqrt{19+6\sqrt{2}}$=$\sqrt{（3\sqrt{2}+1）^{2}}$=3$\sqrt{2}$+1．
故答案为：3$\sqrt{2}$+1

点评 本题主要考查平面向量的应用，根据条件建立坐标系，利用向量与三角函数的综合问题是解决本题的关键．综合性较强，难度较大．