
| A. | p∧q | B. | ¬p | C. | p∧(¬q) | D. | (¬p)∧(¬q) |
分析 分别判定命题p、q的真假,再根据复合命题真假的真值表判定,
解答 解:满足条件的正方形ABCD,如下图示: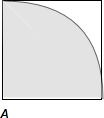
其中满足动点M到定点A的距离|MA|≤1的平面区域如图中阴影所示:
则正方形的面积S正方形=1阴影部分的面积为$\frac{π}{4}$,故动点P到定点A的距离|MA|≤1的概率P=$\frac{π}{4}$.
故命题p为真命题.
对于函数f(x)=x+$\frac{4}{x}$,则f(x)在区间[1,$\frac{3}{2}$]上单调递减,
f(x)的最小值为f($\frac{3}{2}$)≠4,故命题q为假命题.
所以:p∧q为假命题;¬p假命题;p∧(¬q)真命题;(¬p)∧(¬q)假命题;
故选:C
点评 本题考查了复合命题真假的判定,解题的关键是要把每个命题的真假给与正确判断,属于中档题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
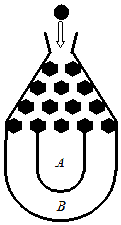 将一个半径适当的小球放入如图所示的容器最上方的入口处,小球将自由下落.小球在下落的过程中,将3次遇到黑色障碍物,最后落入A袋或B袋中.已知小球每次遇到黑色障碍物时,向左、右两边下落的概率都是$\frac{1}{2}$.
将一个半径适当的小球放入如图所示的容器最上方的入口处,小球将自由下落.小球在下落的过程中,将3次遇到黑色障碍物,最后落入A袋或B袋中.已知小球每次遇到黑色障碍物时,向左、右两边下落的概率都是$\frac{1}{2}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
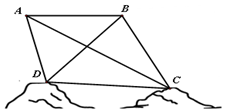 为绘制海底地貌图,测量海底两点C,D间的距离,海底探测仪沿水平方向在A,B两点进行测量,A,B,C,D在同一个铅垂平面内.海底探测仪测得∠BAC=30°,∠DAC=45°,∠ABD=45°,∠DBC=75°,同时测得$AB=\sqrt{3}$海里.
为绘制海底地貌图,测量海底两点C,D间的距离,海底探测仪沿水平方向在A,B两点进行测量,A,B,C,D在同一个铅垂平面内.海底探测仪测得∠BAC=30°,∠DAC=45°,∠ABD=45°,∠DBC=75°,同时测得$AB=\sqrt{3}$海里.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{2e-3}{2e}$ | B. | $\frac{3}{2e}$ | C. | $\frac{{e}^{e}{-e}^{2}+e-1}{e}$ | D. | $\frac{e-1}{e+1}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | $\frac{1}{2}$ | C. | $\frac{1}{4}$ | D. | $\frac{1}{8}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com