
| A. | (-∞,e] | B. | [0,e] | C. | (-∞,e) | D. | [0,e) |
分析 由f(x)的导函数形式可以看出,需要对k进行分类讨论来确定导函数为0时的根.
解答 解:∵函数f(x)=$\frac{{e}^{x}}{{x}^{2}}$-k($\frac{2}{x}$+lnx),
∴函数f(x)的定义域是(0,+∞)
∴f′(x)=$\frac{{e}^{x}{x}^{2}-2x{e}^{x}}{{x}^{4}}$-k(-$\frac{2}{{x}^{2}}$+$\frac{1}{x}$)=$\frac{({e}^{x}-kx)(x-2)}{{x}^{3}}$
∵x=2是函数f(x)的唯一一个极值点
∴x=2是导函数f′(x)=0的唯一根.
∴ex-kx=0在(0,+∞)无变号零点,
令g(x)=ex-kx
g′(x)=ex-k
①k≤0时,g′(x)>0恒成立.g(x)在(0,+∞)时单调递增的
g(x)的最小值为g(0)=1,g(x)=0无解
②k>0时,g′(x)=0有解为:x=lnk
0<x<lnk时,g′(x)<0,g(x)单调递减
lnk<x时,g′(x)>0,g(x)单调递增
∴g(x)的最小值为g(lnk)=k-klnk
∴k-klnk>0
∴k<e,
由y=ex和y=ex图象,它们切于(1,e),
综上所述,k≤e.
故选C
点评 本题考查由函数的导函数确定极值问题.对参数需要进行讨论.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:选择题
| A. | $\frac{{x}^{2}}{4}$+$\frac{{y}^{2}}{5}$=1 | B. | $\frac{{x}^{2}}{16}$+$\frac{{y}^{2}}{25}$=1 | C. | $\frac{{x}^{2}}{5}$+$\frac{{y}^{2}}{4}$=1 | D. | $\frac{{x}^{2}}{25}$+$\frac{{y}^{2}}{16}$=1 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,-3)∪(-3,0] | B. | (-∞,-3)∪(-3,1] | C. | (-3,0] | D. | (-3,1] |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{π}{6}$ | B. | $\frac{π}{3}$ | C. | $\frac{2π}{3}$ | D. | $\frac{5π}{6}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ?x∈R,x2+5x≥6 | B. | ?x∈R,x2+5x=6 | C. | ?x0∈R,x02+5x0≥6 | D. | ?x∈R,x02+5x0<6 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
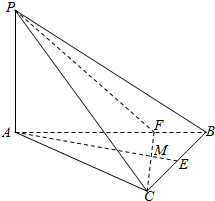 在三棱锥P-ABC中,PA⊥平面ABC,△ABC是直角三角形,AC⊥CB,PA=2,CA=2$\sqrt{3}$,CB=2,E为BC的中点,CF⊥AB于点F,CF交AE于点M.
在三棱锥P-ABC中,PA⊥平面ABC,△ABC是直角三角形,AC⊥CB,PA=2,CA=2$\sqrt{3}$,CB=2,E为BC的中点,CF⊥AB于点F,CF交AE于点M.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com