
| A. | $\frac{{x}^{2}}{4}$+$\frac{{y}^{2}}{5}$=1 | B. | $\frac{{x}^{2}}{16}$+$\frac{{y}^{2}}{25}$=1 | C. | $\frac{{x}^{2}}{5}$+$\frac{{y}^{2}}{4}$=1 | D. | $\frac{{x}^{2}}{25}$+$\frac{{y}^{2}}{16}$=1 |
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源:2017届重庆市高三文上适应性考试一数学试卷(解析版) 题型:解答题
选修4-5:不等式选讲
设函数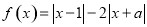 .
.
(1)当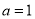 时,求不等式
时,求不等式 的解集;
的解集;
(2)若不等式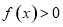 ,在
,在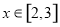 上恒成立,求
上恒成立,求 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
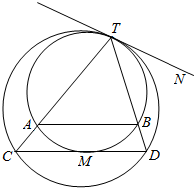 如图所示,两个圆相内切于点T,公切线为TN,外圆的弦TC,TD分别交内圆于A、B两点,并且外圆的弦CD恰切内圆于点M.
如图所示,两个圆相内切于点T,公切线为TN,外圆的弦TC,TD分别交内圆于A、B两点,并且外圆的弦CD恰切内圆于点M.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
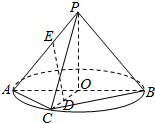 如图,圆锥的轴截面PAB是等腰直角三角形,AB的中点为O,C是底面圆周上异于A,B的任意一点,D为线段OC的中点,E为母线PA上一点,且AE=3EP.
如图,圆锥的轴截面PAB是等腰直角三角形,AB的中点为O,C是底面圆周上异于A,B的任意一点,D为线段OC的中点,E为母线PA上一点,且AE=3EP.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
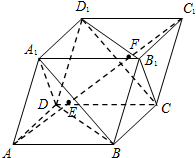 如图,已知平行六面体ABCD-A1B1C1D1中,AC1与平面A1BD、CB1D1交于点E、F两点.设K为△B1CD1的外心,则VK-BED:${V_{{A_1}-BFD}}$=$\frac{1}{3}$.
如图,已知平行六面体ABCD-A1B1C1D1中,AC1与平面A1BD、CB1D1交于点E、F两点.设K为△B1CD1的外心,则VK-BED:${V_{{A_1}-BFD}}$=$\frac{1}{3}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
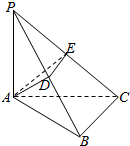 如图,△ABC是直角三角形,∠ABC=90°,AP⊥平面ABC,且AP=AB,点D是PB的中点,点E是PC上的一点,
如图,△ABC是直角三角形,∠ABC=90°,AP⊥平面ABC,且AP=AB,点D是PB的中点,点E是PC上的一点,查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 在直三棱柱ABC-A1B1C1中,AB=AC=AA1=2,∠BAC=$\frac{π}{2}$,E、F依次为CC1和BC的中点:
在直三棱柱ABC-A1B1C1中,AB=AC=AA1=2,∠BAC=$\frac{π}{2}$,E、F依次为CC1和BC的中点:查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,e] | B. | [0,e] | C. | (-∞,e) | D. | [0,e) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com