Question

16．已知在△ABC中，三角A，B，C的对边分别为a，b，c，其满足（a-3b）cosC=c（3cosB-cosA），AF=2FC，则$\frac{AB}{BF}$的取值范围为（2，+∞）．

Answer 1

分析 由正弦定理，两角和的正弦函数公式，三角形内角和定理，诱导公式化简已知可求b=3a，结合AF=2FC，可得CF=a，AF=2a，由余弦定理，三角函数恒等变换的应用可得：$\frac{AB}{BF}$=$\sqrt{\frac{1}{si{n}^{2}\frac{C}{2}}+3}$，结合范围0$＜\frac{C}{2}＜\frac{π}{2}$，即可计算得解．

解答 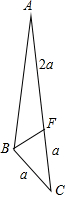解：∵（a-3b）cosC=c（3cosB-cosA），
∴sinAcosC-3sinBcosC=3sinCcosB-sinCcosA，
∴sin（A+C）=3sin（B+C），
∴sinB=3sinA，可得：b=3a，
∵如右图所示，AF=2FC，
∴CF=a，AF=2a，
∴则由余弦定理可得：$\frac{AB}{BF}$=$\sqrt{\frac{{a}^{2}+（3a）^{2}-2×a×3a×cosC}{{a}^{2}+{a}^{2}-2a•a•cosC}}$=$\sqrt{\frac{5-3cosC}{1-cosC}}$
=$\sqrt{\frac{5-3（1-2si{n}^{2}\frac{C}{2}）}{2si{n}^{2}\frac{C}{2}}}$=$\sqrt{\frac{2+6si{n}^{2}\frac{C}{2}}{2si{n}^{2}\frac{C}{2}}}$=$\sqrt{\frac{1}{si{n}^{2}\frac{C}{2}}+3}$，
∵0＜C＜π，0$＜\frac{C}{2}＜\frac{π}{2}$，$\frac{1}{si{n}^{2}\frac{C}{2}}$∈（1，+∞），
∴$\frac{AB}{BF}$=$\sqrt{\frac{1}{si{n}^{2}\frac{C}{2}}+3}$∈（2，+∞）．
故答案为：（2，+∞）．

点评 本题主要考查了正弦定理，两角和的正弦函数公式，三角形内角和定理，诱导公式，余弦定理，三角函数恒等变换的应用在解三角形中的综合应用，考查了计算能力和转化思想，属于中档题．