Question

11．如图，在五面体ABCDEF中，AB∥CD∥EF，CD=EF=CF=2AB=2AD=2，∠ACF=60°，AD⊥CD，平面CDEF⊥平面ABCD，P是BC的中点，
（1）求异面直线BE与PF所成角的余弦值；
（2）在直线EF上，是否存在一点Q，使得PQ∥平面EBD，若存在，求出该点；若不存在请说明理由．

Answer 1

分析 （1）推导出四边形CDEF为菱形，取EF的中点G，连接GD，则GD⊥EF，GD⊥CD，从而GD⊥平面ABCD，以D为原点，DA，DC，DG的方向为x，y，z轴，建立空间直角坐标系，利用向量法能求出异面直线BE与PF所成角的余弦值．
（2）存在，该点即为EF中点G，连结CE、DF交于点H，推导出平面PGH∥平面EBD，从而PG∥平面EBD．

解答 解：（1）∵CD∥EF，CD=EF=CF=2，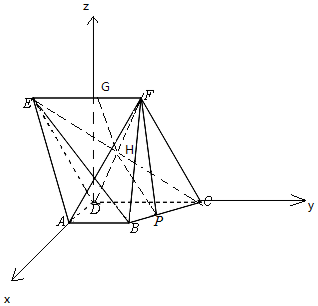
∴四边形CDEF为菱形，
∵∠DCF=60°，∴△DEF为正三角形，取EF的中点G，连接GD，则GD⊥EF，
∴GD⊥CD，∵平面CDEF⊥平面ABCD，GD?平面CDEF，
CD=平面CDEF∩平面ABCD，∴GD⊥平面ABCD，
∵AD⊥CD，∴DA，DC，DG两两垂直，…（2分）
以D为原点，DA，DC，DG的方向为x，y，z轴，建立空间直角坐标系，
∵CD=EF=CF=2，AB=AD=1，
∴A（1，0，0），B（1，1，0），C（0，2，0），E（0，-1，$\sqrt{3}$），F（0，1，$\sqrt{3}$），$P（{\frac{1}{2}，\frac{3}{2}，0}）$，
∴$\overrightarrow{BE}=（{-1，-2，\sqrt{3}}），\overrightarrow{PF}=（{-\frac{1}{2}，-\frac{1}{2}，\sqrt{3}}）$，
cos＜$\overrightarrow{BE}$，$\overrightarrow{PF}$＞=$\frac{\overrightarrow{BE}•\overrightarrow{PF}}{|\overrightarrow{BE}|•|\overrightarrow{PF}|}$=$\frac{\frac{9}{2}}{\sqrt{8•\frac{7}{2}}}$=$\frac{9\sqrt{7}}{28}$．
∴异面直线BE与PF所成角的余弦值为$\frac{9\sqrt{7}}{28}$．
（2）存在，该点即为EF中点G，
连结CE、DF交于点H，
∵PH∥EB，GH∥ED，EB∩ED=E，
PH，GH?平面PGH，EB，ED?平面EBD，
∴平面PGH∥平面EBD，∴PG∥平面EBD．

点评 本题考查线面角的余弦值的求法，考查满足线面平行的点的位置的确定与求法，考查空间中线线、线面、面面间的位置关系等基础知识，考查推理论证能力、运算求解能力，考查化归与转化思想、函数与方程思想，是中档题．