
【题目】已知椭圆C: ![]() (a>b>0)的离心率为
(a>b>0)的离心率为 ![]() ,左、右焦点分别为F1 , F2 , 点G在椭圆C上,且
,左、右焦点分别为F1 , F2 , 点G在椭圆C上,且 ![]()
![]() =0,△GF1F2的面积为2.
=0,△GF1F2的面积为2. 
(1)求椭圆C的方程;
(2)直线l:y=k(x﹣1)(k<0)与椭圆Γ相交于A,B两点.点P(3,0),记直线PA,PB的斜率分别为k1 , k2 , 当 ![]() 最大时,求直线l的方程.
最大时,求直线l的方程.
【答案】
(1)解:∵椭圆 ![]() (a>b>0)的离心率为
(a>b>0)的离心率为 ![]() ,
,
∴e= ![]() ,①
,①
∵左右焦点分别为F1、F2,点G在椭圆上,
∴| ![]() |+|
|+| ![]() |=2a,②
|=2a,②
∵ ![]()
![]() =0,△GF1F2的面积为2,
=0,△GF1F2的面积为2,
∴| ![]() |2+|
|2+| ![]() |2=4c2,③
|2=4c2,③
![]() ,④
,④
联立①②③④,得a2=4,b2=2,
∴椭圆C的方程为 ![]() ;
;
(2)解:联立  ,得(1+2k2)x2﹣4k2x+2k2﹣4=0.
,得(1+2k2)x2﹣4k2x+2k2﹣4=0.
设A(x1,y1),B(x2,y2),
∴ ![]() .
.
![]()
= 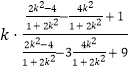 =
= ![]()
= ![]() ,当且仅当
,当且仅当 ![]() 时,取得最值.
时,取得最值.
此时l:y= ![]()
【解析】(1)由椭圆的离心率为 ![]() 、点G在椭圆上、
、点G在椭圆上、 ![]()
![]() =0及△GF1F2的面积为2列式求得a2=4,b2=2,则椭圆方程可求;(2)联立直线方程和椭圆方程,化为关于x的一元二次方程,利用根与系数的关系得到A,B两点横坐标的和与积,把
=0及△GF1F2的面积为2列式求得a2=4,b2=2,则椭圆方程可求;(2)联立直线方程和椭圆方程,化为关于x的一元二次方程,利用根与系数的关系得到A,B两点横坐标的和与积,把 ![]() 转化为含有k的代数式,利用基本不等式求得使
转化为含有k的代数式,利用基本不等式求得使 ![]() 取得最大值的k,则直线Γ的方程可求.
取得最大值的k,则直线Γ的方程可求.
【考点精析】根据题目的已知条件,利用椭圆的标准方程的相关知识可以得到问题的答案,需要掌握椭圆标准方程焦点在x轴:![]() ,焦点在y轴:
,焦点在y轴:![]() .
.


 导学与测试系列答案
导学与测试系列答案 新非凡教辅冲刺100分系列答案
新非凡教辅冲刺100分系列答案科目:高中数学 来源: 题型:
【题目】已知一组数据的频率分布直方图如图所示.求众数、中位数、平均数( ) 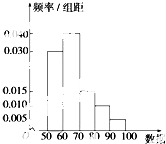
A.63、64、66
B.65、65、67
C.65、64、66
D.64、65、64
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,抛物线关于x轴对称,它的顶点在坐标原点,点P(1,2),A(x1 , y1),B(x2 , y2)均在抛物线上. 
(1)写出该抛物线的方程及其准线方程;
(2)当PA与PB的斜率存在且倾斜角互补时,求y1+y2的值及直线AB的斜率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=x2+2ax+2,x∈[﹣5,5].
(1)当a=﹣1时,求函数f(x)的最大值和最小值.
(2)函数y=f(x)在区间[﹣5,5]上是单调函数,求实数a的范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,平面四边形ABCD中,AB= ![]() ,AD=2
,AD=2 ![]() ,CD=
,CD= ![]() ,∠CBD=30°,∠BCD=120°.
,∠CBD=30°,∠BCD=120°.
(1)求BD的长;
(2)求∠ADC的度数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆E: ![]() =1(a>b>0)的离心率e=
=1(a>b>0)的离心率e= ![]() ,并且经过定点P(
,并且经过定点P( ![]() ,
, ![]() ). (Ⅰ)求椭圆E的方程;
). (Ⅰ)求椭圆E的方程;
(Ⅱ)问是否存在直线y=﹣x+m,使直线与椭圆交于A、B两点,满足OA⊥OB,若存在求m值,若不存在说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com