
【题目】已知以点![]() 为圆心的圆过原点O,与x轴另一个交点为M,与y轴另一个交点为N,
为圆心的圆过原点O,与x轴另一个交点为M,与y轴另一个交点为N,
(1)求证:△MON的面积为定值;
(2)直线4x+ y-4=0与圆C交于点A、B,若![]() ,求圆C的方程
,求圆C的方程
(3)若直线l:x+ y -5=0和圆C交于点A,B两点,且AB=![]() ,求圆心C的坐标。
,求圆心C的坐标。
【答案】(1)证明见解析;(2)![]() ;(3)(1,2)或(2,1).
;(3)(1,2)或(2,1).
【解析】
试题分析:(1)关键是求出![]() 的面积,首先写出圆
的面积,首先写出圆![]() 的方程
的方程![]() ,可化简后分别令
,可化简后分别令![]() 和
和![]() 求得
求得![]() 的坐标,从而得
的坐标,从而得![]() 的面积;(2)由
的面积;(2)由![]() ,知
,知![]() 在
在![]() 的中垂线上,从而
的中垂线上,从而![]() ,因此可得
,因此可得![]() 斜率,由此可得
斜率,由此可得![]() ,得圆
,得圆![]() 方程;(3)已知直线与圆相交弦长,可由垂径定理求得弦长,即先求得圆心
方程;(3)已知直线与圆相交弦长,可由垂径定理求得弦长,即先求得圆心![]() 到直线
到直线![]() 的距离
的距离![]() ,由勾股定列出关于
,由勾股定列出关于![]() 的方程,解得可得圆心坐标.
的方程,解得可得圆心坐标.
试题解析:(1)由题设知,圆C的方程为![]() ,化简得
,化简得![]() ,当y=0时,x=0或2t,则
,当y=0时,x=0或2t,则![]() ;当x=0时,y=0或
;当x=0时,y=0或![]() ,则
,则![]() , ∴
, ∴![]() 为定值
为定值
(2)∵![]() ,则原点O在AB的中垂线上,设AB的中点为H,则CH⊥AB,∴C、H、O三点共线,则直线OC的斜率
,则原点O在AB的中垂线上,设AB的中点为H,则CH⊥AB,∴C、H、O三点共线,则直线OC的斜率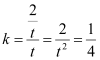 ,∴t=2
,∴t=2![]() (负舍)
(负舍)
∴圆心C(2![]() ,
, ![]() )∴圆C的方程为
)∴圆C的方程为![]()
(3)d= ,r=
,r=![]() ,弦长为
,弦长为![]() ,列出方程:
,列出方程:
 ,令
,令![]() ,方程可化为
,方程可化为![]() ,解得
,解得
m=3或-13(舍),则t=1或2,所以圆心C(1,2)或(2,1).


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】如图(a),在直角梯形ABCD中,∠ADC=90°,CD∥AB,AB=8,AD=CD=4,将△ADC沿AC折起,使平面ADC⊥平面ABC,得到几何体D-ABC,如图(b)所示.

(1)求证:BC⊥平面ACD;
(2)求几何体D-ABC的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某货轮匀速行驶在相距![]() 海里的甲、乙两地间运输货物,运输成本由燃料费用和其他费用组成.已知该货轮每小时的燃料费用与其航行速度的平方成正比(比例系数为
海里的甲、乙两地间运输货物,运输成本由燃料费用和其他费用组成.已知该货轮每小时的燃料费用与其航行速度的平方成正比(比例系数为![]() ),其他费用为每小时
),其他费用为每小时![]() 元,且该货轮的最大航行速度为
元,且该货轮的最大航行速度为![]() 海里/小时.
海里/小时.
(1)请将从甲地到乙地的运输成本![]() (元)表示为航行速度
(元)表示为航行速度![]() (海里/小时)的函数;
(海里/小时)的函数;
(2)要使从甲地到乙地的运输成本最少,该货轮应以多大的航行速度行驶?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在直角坐标系![]() 中,直线
中,直线![]() 的方程是
的方程是![]() ,圆
,圆![]() 的参数方程是
的参数方程是![]() (
(![]() 为参数).以原点
为参数).以原点![]() 为极点,
为极点,![]() 轴的非负半轴为极轴建立极坐标系.
轴的非负半轴为极轴建立极坐标系.
(1)分别求直线![]() 与圆
与圆![]() 的极坐标方程;
的极坐标方程;
(2)射线![]() :
:![]() (
(![]() )与圆
)与圆![]() 的交点为
的交点为![]() 、
、![]() 两点,与直线
两点,与直线![]() 交于点
交于点![]() ,射线
,射线![]() :
:![]() 与圆
与圆![]() 交于
交于![]() ,
,![]() 两点,与直线
两点,与直线![]() 交于点
交于点![]() ,求
,求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(1)求过直线l1:x-2y+3=0与直线l2:2x+3y-8=0的交点,且到点P(0,4)的距离为2的直线方程.
(2)设直线l的方程为(a+1)x+y+2-a=0(a∈R).若l在两坐标轴上的截距相等,求l的方程;
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲、乙两人玩数字游戏,先由甲任想一个数字记为![]() ,再由乙猜甲刚才想的数字把乙想的数字记为
,再由乙猜甲刚才想的数字把乙想的数字记为![]() ,且
,且![]() ,
, ![]() ,记
,记![]() .
.
(1)求![]() 的概率;
的概率;
(2)若![]() ,则称“甲乙心有灵犀”,求“甲乙心有灵犀”的概率.
,则称“甲乙心有灵犀”,求“甲乙心有灵犀”的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com