
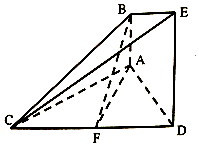
 如图的几何体中,AB⊥平面ACD,DE⊥平面ACD,△ACD为等边三角形,AD=DE=2AB=2,F为CD的中点.
如图的几何体中,AB⊥平面ACD,DE⊥平面ACD,△ACD为等边三角形,AD=DE=2AB=2,F为CD的中点.分析 (1)通过取CE的中点G,利用三角形的中位线定理和平行四边形的性质及线面平行的判定定理即可证明;
(2)利用三棱锥的体积公式计算,即可求A到平面BCE的距离.
解答 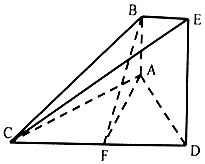 (1)证明:取CE的中点G,连接FG、BG.
(1)证明:取CE的中点G,连接FG、BG.
∵F为CD的中点,∴GF∥DE且$GF=\frac{1}{2}DE$.
∵AB⊥平面ACD,DE⊥平面ACD,
∴AB∥DE,∴GF∥AB,
又$AB=\frac{1}{2}DE$,∴GF=AB.
∴四边形GFAB为平行四边形,则AF∥BG.
∵AF?平面BCE,BG?平面BCE,∴AF∥平面BCE.
(2)连接AE,设A到平面BCE的距离为h,
在△BCE中,$BC=BE=\sqrt{5}$,$CE=2\sqrt{2}$,
∴${S_{△BCE}}=\frac{1}{2}×2\sqrt{2}×\sqrt{3}=\sqrt{6}$,
又$CH=\sqrt{3}$,${S_{△ABE}}=\frac{1}{2}×1×2=1$,
∴由VA-BCE=VC-ABE,即$\frac{1}{3}•h•{S_{△BCE}}=\frac{1}{3}•CH•{S_{△ABE}}$(CH为正△ACD的高),
∴$h=\frac{{\sqrt{2}}}{2}$
即点A到平面BCE的距离为$\frac{{\sqrt{2}}}{2}$.
点评 熟练掌握线面平行的判定定理和性质定理及棱锥的体积计算公式是解题的关键.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 大前提错误 | B. | 小前提错误 | C. | 推理形式错误 | D. | 是正确的 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | $\frac{\sqrt{2}}{2}$ | C. | 1 | D. | $\sqrt{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [$\frac{π}{12}$,$\frac{π}{4}$] | B. | [$\frac{π}{6}$,$\frac{5π}{12}$) | C. | [$\frac{π}{6}$,$\frac{π}{3}$] | D. | ($\frac{π}{6}$,$\frac{π}{4}$] |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com