
分析 (I)求导数,根据已知条件f(x)在x=1处的切线方程过坐标原点,可求a,b的关系;
(II)函数f(x)在区间(0,1)上为增函数,只要f′(x)≥0在区间(0,1)上恒成立,利用常数分离法进行求解;
(Ⅲ)这个证明题可以利用一个恒等式,sinx<x,然后对$\sum_{k=1}^{n}$sin$\frac{1}{(k+1)^{2}}$从第三项开始进行放缩,然后进行证明.
解答 (I)解:∵f(x)=asin(1-x)+lnx+b,
∴f′(x)=-acos(1-x)+$\frac{1}{x}$,
∴f′(1)=-a+1,
∵f(1)=b,
∴f(x)在x=1处的切线方程为y-b=(-a+1)(x-1),
∵f(x)在x=1处的切线方程过坐标原点,
∴0-b=(-a+1)(0-1),
∴b=1-a;
(Ⅱ)∵f(x)=asin(1-x)+lnx+1-a,
∴f′(x)=acos(1-x)×(-1)+$\frac{1}{x}$,
函数f(x)在区间(0,1)上为增函数,只要f′(x)≥0在区间(0,1)上恒成立,
∴acos(1-x)×(-1)+$\frac{1}{x}$≥0,
∴a≤$\frac{1}{xcos(1-x)}$,
设h(x)=xcos(1-x),0<1-x<1,
∵h′(x)=cos(1-x)+xsin(1-x)>0,
∴h(x)在(0,1)增函数,
∴h(x)<h(1)=1,
∴a≤1;
(Ⅲ)证明:∵0<$\frac{1}{(k+1)^{2}}$<1,
∵sinx<x在x∈(0,1)上恒成立,
∴$\sum_{k=1}^{n}$sin$\frac{1}{(k+1)^{2}}$=sin$\frac{1}{{2}^{2}}$+sin$\frac{1}{{3}^{2}}$+…+sin$\frac{1}{(n+1)^{2}}$≤$\frac{1}{{2}^{2}}$+$\frac{1}{{3}^{2}}$+…+$\frac{1}{(n+1)^{2}}$
<$\frac{1}{4}$+$\frac{1}{9}$+$\frac{1}{16}$+$\frac{1}{4×5}$+$\frac{1}{5×6}$+…+$\frac{1}{n(n+1)}$=$\frac{97}{144}$-$\frac{1}{n+1}$<$\frac{97}{144}$<ln2,
∴$\sum_{k=1}^{n}$sin$\frac{1}{(k+1)^{2}}$<ln2.
点评 第一问利用导数可以很容易解决,第二问利用了常数分离法进行证明,第三问需要进行放缩证明,主要利用sinx<x进行证明,此题难度比较大,计算量比较大.


科目:高中数学 来源: 题型:选择题
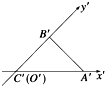 水平放置的△ABC的斜二测直观图△A′B′C′如图所示,已知A′C′=3,B′C′=2,则△ABC的面积为( )
水平放置的△ABC的斜二测直观图△A′B′C′如图所示,已知A′C′=3,B′C′=2,则△ABC的面积为( )| A. | 6 | B. | 3 | C. | $\frac{{3\sqrt{2}}}{2}$ | D. | $3\sqrt{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| 优、良、中 | 差 | 总计 | |
| 实验班 | 48 | 2 | 50 |
| 对比班 | 38 | 12 | 50 |
| 总计 | 86 | 14 | 100 |
| A. | 有关 | B. | 无关 | C. | 关系不明确 | D. | 以上都不正确 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com