
【题目】
已知函数y=4cos2x-4![]() sinxcosx-1(x∈R).
sinxcosx-1(x∈R).
(1)求出函数的最小正周期;
(2)求出函数的最大值及其相对应的x值;
(3)求出函数的单调增区间;
(4)求出函数的对称轴.
 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案科目:高中数学 来源: 题型:
【题目】某校团委对“学生性别与中学生追星是否有关”作了一次调查,利用![]() 列联表,由计算得
列联表,由计算得![]() ,参照下表:
,参照下表:
| 0.01 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
得到正确结论是( )
A. 有99%以上的把握认为“学生性别与中学生追星无关”
B. 有99%以上的把握认为“学生性别与中学生追星有关”
C. 在犯错误的概率不超过0.5%的前提下,认为“学生性别与中学生追星无关”
D. 在犯错误的概率不超过0.5%的前提下,认为“学生性别与中学生追星有关”
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某同学在研究函数f(x)=![]() (x∈R)时,分别给出下面几个结论:
(x∈R)时,分别给出下面几个结论:
①等式f(-x)=-f(x)在x∈R时恒成立;
②函数f(x)的值域为(-1,1);
③若x1≠x2,则一定有f(x1)≠f(x2);
④方程f(x)=x在R上有三个根.
其中正确结论的序号有______.(请将你认为正确的结论的序号都填上)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,四边形EFGH为空间四边形ABCD的一个截面,若截面为平行四边形.
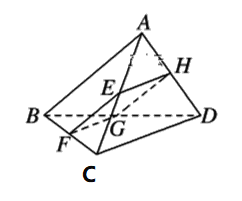
(1)求证:AB∥平面EFGH
(2)若AB=4,CD=6,求四边形EFGH周长的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设某大学的女生体重y(单位:kg)与身高x(单位:cm)具有线性相关关系,根据一组样本数据(xi,yi)(i=1,2,…,n),用最小二乘法建立的回归方程为![]() =0.85x-85.71,则下列结论中不正确的是
=0.85x-85.71,则下列结论中不正确的是
A. y与x具有正的线性相关关系
B. 回归直线过样本点的中心(![]() ,
,![]() )
)
C. 若该大学某女生身高增加1cm,则其体重约增加0.85kg
D. 若该大学某女生身高为170cm,则可断定其体重比为58.79kg
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图1,已知四边形BCDE为直角梯形,![]() ,
,![]() ,且
,且![]() ,A为BE的中点
,A为BE的中点![]() 将
将![]() 沿AD折到
沿AD折到![]() 位置
位置![]() 如图
如图![]() ,连结PC,PB构成一个四棱锥
,连结PC,PB构成一个四棱锥![]() .
.

![]() Ⅰ
Ⅰ![]() 求证
求证![]() ;
;
![]() Ⅱ
Ⅱ![]() 若
若![]() 平面ABCD.
平面ABCD.
![]() 求二面角
求二面角![]() 的大小;
的大小;
![]() 在棱PC上存在点M,满足
在棱PC上存在点M,满足![]() ,使得直线AM与平面PBC所成的角为
,使得直线AM与平面PBC所成的角为![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com