
分析 应用线面垂直和面面垂直的判定定理,即可判断①;
通过举例x=1,即可判断②;求出原命题的逆命题,考虑m=0,即可判断③;
由三角函数的图象变换,注意自变量x的变化,即可判断④.
解答 解:对①,由m⊥α,n?β,α⊥β推出m∥n或m,n异面,反之若m∥n,可得n⊥α,再由面面垂直的判定定理,推出α⊥β,故“α⊥β”是“m∥n”的必要不充分条件,正确;
对②,若x=1,则log2x=log3x=0,对于?x∈(0,+∞),log2x<log3x不成立,故不正确;
对③“若am2<bm2,则a<b”的逆命题为“若a<b,则am2<bm2”若m=0则不正确;
对④,把函数$y=3sin(2x+\frac{π}{3})$的图象向右平移$\frac{π}{6}$个单位,
可得到y=3sin[2(x-$\frac{π}{6}$)+$\frac{π}{3}$],即为y=3sin2x的图象.故正确.
故答案为:①④.
点评 本题考查命题的真假判断和应用,考查空间线面垂直和面面垂直的判定和性质,考查四种命题的真假判断和充分必要条件的判断,以及三角函数的图象变换,考查推理和判断能力,属于基础题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | 1 | C. | -$\frac{3}{2}$ | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $[{-\frac{5}{2},-1})∪[2,5)$ | B. | $[{-1,-\frac{2}{3}})∪[5,10)$ | C. | $({-\frac{4}{3},-1}]∪[5,10)$ | D. | $[{-\frac{4}{3},-1}]∪[5,10)$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
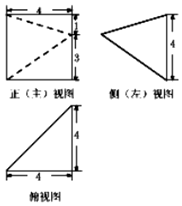
| A. | $\sqrt{33}$ | B. | $\sqrt{17}$ | C. | $\sqrt{41}$ | D. | $\sqrt{42}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com