
分析 (1)配方,分类讨论,即可求f(x)在区间[0,m]上的最小值;
(2)根据解析式,作出函数f(|x|)的图象,根据从左到右下降对应函数的单调递减区间;
(3)线y=x+a与y=x2+4x+3相切时,a=$\frac{3}{4}$,直线过(0,3)时,a=3,即可得出结论.
解答 解:(1)f(x)=x2-4x+3=(x-2)2-1,
m<2,∴x=m时,f(x)在区间[0,m]上的最小值为m2-4m+3;
m≥2,∴x=2时,f(x)在区间[0,m]上的最小值为-1;
∴f(x)在区间[0,m]上的最小值为$\left\{\begin{array}{l}{{m}^{2}-4m+3,m<2}\\{-1,m≥2}\end{array}\right.$;
(2)函数f(|x|)=x2-4|x|+3的图象如图所示 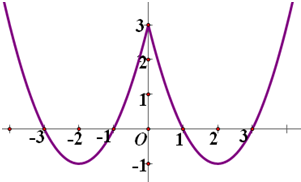
函数f(|x|)=x2-4|x|+3的单调递减区间是(-∞,-2)和(0,2);
(3)直线y=x+a与y=x2+4x+3相切时,a=$\frac{3}{4}$,
直线过(0,3)时,a=3,
∵关于x的方程f(|x|)-a=x至少有三个不相等的实根,∴$\frac{3}{4}$≤a≤3.
点评 此题主要考查二次函数的性质及其图象的应用,是一道中档题,根据二次函数图象和性质,画出函数的图象是解答的关键.


 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
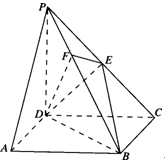 如图所示,在四棱锥P-ABCD中,底面ABCD是正方形,侧棱PD⊥底面ABCD,PD=DC=2,E是PC的中点,作EF⊥PB交PB于点F.
如图所示,在四棱锥P-ABCD中,底面ABCD是正方形,侧棱PD⊥底面ABCD,PD=DC=2,E是PC的中点,作EF⊥PB交PB于点F.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com