
分析 由题意可得AC⊥CD,设CD=x,可得AD=$\sqrt{2}$x,AC=x,设∠ACB=α,运用余弦定理,求出BD关于x的关系式,结合基本不等式即可得到所求最大值.
解答  解:AB=2,$BC=2\sqrt{2}$,$AD=\sqrt{2}CD$,$\overrightarrow{AC}\overrightarrow{•CD}=0$,
解:AB=2,$BC=2\sqrt{2}$,$AD=\sqrt{2}CD$,$\overrightarrow{AC}\overrightarrow{•CD}=0$,
可得AC⊥CD,
设CD=x,可得AD=$\sqrt{2}$x,AC=x,
设∠ACB=α,可得BD2=DC2+BC2-2DC•BC•cos(90°+α)
=x2+8-4$\sqrt{2}$x•(-sinα)=x2+8+4$\sqrt{2}$x•sinα,
在△ABC中,可得cosα=$\frac{{x}^{2}+8-4}{4\sqrt{2}x}$=$\frac{{x}^{2}+4}{4\sqrt{2}x}$,
sinα=$\frac{\sqrt{-{x}^{4}+24{x}^{2}-16}}{4\sqrt{2}x}$,
则BD2=x2+8+$\sqrt{-({x}^{2}-12)^{2}+128}$=(x2-12)+$\sqrt{-({x}^{2}-12)^{2}+128}$+20
要求$|{\overrightarrow{BD}}|$的最大值,则x2-12>0,
再由a2+b2≥2ab,可得($\frac{a+b}{2}$)2≤$\frac{{a}^{2}+{b}^{2}}{2}$,(a=b取得等号),
可得a+b≤$\sqrt{2({a}^{2}+{b}^{2})}$.
即有BD2≤$\sqrt{2[({x}^{2}-12)^{2}-({x}^{2}-12)^{2}+128]}$+20=16+20=36,
当x2-12=8,即x=2$\sqrt{5}$时,则$|{\overrightarrow{BD}}|$的最大值为6.
故答案为:6.
点评 本题考查余弦定理的运用,考查向量垂直的条件:数量积为0,以及基本不等式的运用:求最值,考查化简整理的运算能力,属于中档题.


科目:高中数学 来源: 题型:选择题
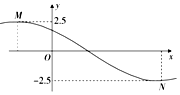 已知函数f(x)=2.5cos(ωx+φ)(ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,M、N两点之间的距离为13,且f(3)=0,若将函数f(x)的图象向右平移t(t>0)个单位长度后所得函数的图象关于坐标原点对称,则t的最小值为( )
已知函数f(x)=2.5cos(ωx+φ)(ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,M、N两点之间的距离为13,且f(3)=0,若将函数f(x)的图象向右平移t(t>0)个单位长度后所得函数的图象关于坐标原点对称,则t的最小值为( )| A. | 7 | B. | 8 | C. | 9 | D. | 10 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a<b<c | B. | c<a<b | C. | b<a<c | D. | c<b<a |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3 | B. | 2 | C. | $\frac{3\sqrt{2}}{4}$ | D. | $\frac{3}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
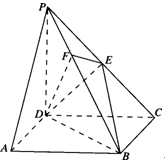 如图所示,在四棱锥P-ABCD中,底面ABCD是正方形,侧棱PD⊥底面ABCD,PD=DC=2,E是PC的中点,作EF⊥PB交PB于点F.
如图所示,在四棱锥P-ABCD中,底面ABCD是正方形,侧棱PD⊥底面ABCD,PD=DC=2,E是PC的中点,作EF⊥PB交PB于点F.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com