
分析 (1)利用定义法判断即可.
(2)利用特特值证明即可.
解答 解:(1)证明:设任意x1,x2∈(-∞,0),且x1<x2,则$f({x_1})-f({x_2})=(-\frac{1}{x_1}-2)-(-\frac{1}{x_2}-2)=\frac{{{x_1}-{x_2}}}{{{x_1}{x_2}}}$
∵x1,x2∈(-∞,0),∴x1x2>0;
又x1<x2,∴x1-x2<0,
所以:$\frac{{{x_1}-{x_2}}}{{{x_1}{x_2}}}<0$,即f(x1)<f(x2),
∴f(x)在区间(-∞,0)上是单调增函数.
2)由题意:f(x)的定义域为(-∞,0)∪(0,+∞);
在定义域上取x1=-1,x2=1,则f(x1)=-1,f(x2)=-3
此时有:x1<x2,但f(x1)>f(x2)
故f(x)在定义域内不是单调增函数.
点评 本题考查了用定义法判断单调性,同时考查了由特殊到一般的思想,采取特殊性证明其不成立即可.属于基础题.


科目:高中数学 来源: 题型:选择题
| A. | $\frac{13}{36}$ | B. | $\frac{12}{25}$ | C. | $\frac{13}{25}$ | D. | $\frac{1}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,设椭圆$C:\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$的左右焦点为F1,F2,上顶点为A,点B和点F2关于F1对称,且AB⊥AF2,A,B,F2三点确定的圆M恰好与直线$x-\sqrt{3}y-3=0$相切.
如图,设椭圆$C:\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$的左右焦点为F1,F2,上顶点为A,点B和点F2关于F1对称,且AB⊥AF2,A,B,F2三点确定的圆M恰好与直线$x-\sqrt{3}y-3=0$相切.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
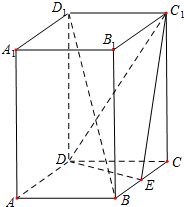 如图,在直四棱柱ABCD-A1B1C1D1中,侧棱AA1的长为3,底面ABCD是边长为2的正方形,E是棱BC的中点.
如图,在直四棱柱ABCD-A1B1C1D1中,侧棱AA1的长为3,底面ABCD是边长为2的正方形,E是棱BC的中点.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{2}{3}$ | B. | $\frac{\sqrt{3}}{3}$ | C. | $\frac{\sqrt{2}}{3}$ | D. | $\frac{1}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -1 | B. | 1 | C. | e | D. | $\frac{1}{e}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com