
分析 ①令a=1,b=0,得出f(1)=f(1)•f(0 ),再结合当x>0时,f(x)>1.得出f(0)=1,
②分类证明:(i)当x>0时,f(x)>1>0成立;(ii)当x=0时,f(x)=f(0)=1>0成立;(iii)当x<0时,令a=x,b=-x,即可证明,
③任意x1,x2∈R,且x1>x2,则f(x1)-f(x2),确定出f(x1)>f(x2)后即可判断出函数f(x)在R上单调递增,
④根据函数为增函数,即可得到3x-x2>0,解得即可.
解答 解:①:令a=1,b=0,则有:f(1+0)=f(1)•f(0)⇒f(1)=f(1)•f(0)⇒f(1)(1-f(0))=0,
∵当x>0时,f(x)>1>0,
∴1-f(0)=0,
∴f(0)=1
②:(i)当x>0时,f(x)>1>0成立;
(ii)当x=0时,f(x)=f(0)=1>0成立;
(iii)当x<0时,令a=x,b=-x,则有:f(x+(-x))=f(x)•f(-x)⇒f(0)=f(x)•f(-x)⇒f(x)•f(-x)=1>0,
∵x<0,
∴-x>0,
∴f(-x)>1>0,
故f(x)>0成立.
综上可得:x∈R时,恒有f(x)>0.
③:f(x)在R上是增函数,证明如下:
设任意x1,x2∈R,且x1>x2,则f(x1)-f(x2)=f(x1-x2+x2)-f(x2)=f(x1-x2)•f(x2)-f(x2)=f(x2)[f(x1-x2)-1]
由②得:x∈R时,恒有f(x)>0,
∴f(x2)>0
又x1>x2,∴x1-x2>0,
由当x>0时,f(x)>1恒成立得:f(x1-x2)>1⇒f(x1-x2)-1>0,
∴f(x2)[f(x1-x2)-1]>0,
即f(x1)>f(x2)
故f(x)在R上是增函数.
④:∵f(x)•f(2x-x2)>1,
∴f(3x-x2)>f(0),
∴3x-x2>0,
解得0<x<3,
故①②正确,
故答案为:①②
点评 本题考查抽象函数求函数值、单调性的判定、及单调性的应用,考查转化.牢牢把握所给的关系式,对式子中的字母准确灵活的赋值,变形构造是解决抽象函数问题常用的思路


 期末金牌卷系列答案
期末金牌卷系列答案 轻松课堂标准练系列答案
轻松课堂标准练系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | 1 | C. | 8 | D. | $\frac{1}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3 | B. | 2 | C. | 1 | D. | 0 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1-i}{2}$ | B. | $\frac{1+i}{2}$ | C. | $\frac{-1-i}{2}$ | D. | $\frac{-1+i}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
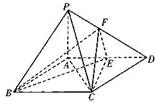 已知四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD为平行四边形,∠ABC+∠ADC=90°,E是线段AD的中点,F在线段PD上运动,记$\frac{PF}{PD}$=λ.
已知四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD为平行四边形,∠ABC+∠ADC=90°,E是线段AD的中点,F在线段PD上运动,记$\frac{PF}{PD}$=λ.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com