
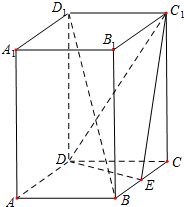
 如图,在直四棱柱ABCD-A1B1C1D1中,侧棱AA1的长为3,底面ABCD是边长为2的正方形,E是棱BC的中点.
如图,在直四棱柱ABCD-A1B1C1D1中,侧棱AA1的长为3,底面ABCD是边长为2的正方形,E是棱BC的中点.分析 以点D为原点,$\overrightarrow{DA},\overrightarrow{DC},\overrightarrow{D{D_1}}$分别为x轴、y轴、z轴的正方向建立空间直角坐标系D-xyz,求出相关点的坐标.(Ⅰ)求出平面C1DE的一个法向量,$\overrightarrow{B{D_1}}=(-2,-2,3)$,通过数量积为0,推出BD1∥平面C1DE;
(Ⅱ)求出平面ABCD的一个法向量,利用向量的数量积求解夹角的余弦函数值,然后求解二面角C1-DE-C的正切值.
(Ⅲ)假设侧棱BB1上是否存在点P,使得CP⊥平面C1DE,设P(2,2,t),利用$\overrightarrow{CP}$与$\overrightarrow n$共线,列出不等式组,求解即可.
解答 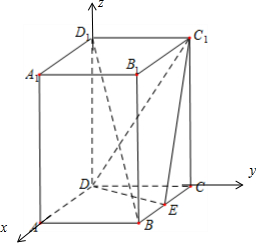 解:以点D为原点,$\overrightarrow{DA},\overrightarrow{DC},\overrightarrow{D{D_1}}$分别为x轴、y轴、z轴的正方向建立空间直角坐标系D-xyz,则B(2,2,0),C(0,2,0),C1(0,2,3),D1(1,2,0),∵DC⊥AD是棱△ABC的中点,
解:以点D为原点,$\overrightarrow{DA},\overrightarrow{DC},\overrightarrow{D{D_1}}$分别为x轴、y轴、z轴的正方向建立空间直角坐标系D-xyz,则B(2,2,0),C(0,2,0),C1(0,2,3),D1(1,2,0),∵DC⊥AD是棱△ABC的中点,
∴E(1,2,0),$\overrightarrow{D{C_1}}=(0,2,3),\overrightarrow{DE}=(1,2,0)$
(Ⅰ)设平面C1DE的一个法向量为$\overrightarrow n=(x,y,z)$,
则$\left\{\begin{array}{l}\overrightarrow n•\overrightarrow{DE}=0\\ \overrightarrow n•\overrightarrow{D{C_1}}=0\end{array}\right.⇒\left\{\begin{array}{l}2y+3z=0\\ x+2y=0\end{array}\right.⇒\overrightarrow n=(6,-3,2)$,
∵$\overrightarrow{B{D_1}}=(-2,-2,3)$,∴$\overrightarrow n•\overrightarrow{DE}=-2×6+2×3+3×2=0$,
∴$\overrightarrow n⊥\overrightarrow{DE}$,又DE?平面C1DE,∴BD1∥平面C1DE;
(Ⅱ)平面ABCD的一个法向量为$\overrightarrow{C{C_1}}=(0,0,3)$,
∴$cos<\overrightarrow{C{C_1}},\overrightarrow n>=\frac{{\overrightarrow{C{C_1}}•\overrightarrow n}}{{|\overrightarrow{C{C_1}}|•|\overrightarrow n|}}=\frac{2}{7}$,$sin<\overrightarrow{C{C_1}},\overrightarrow n>=\frac{{3\sqrt{5}}}{7}$,$tan<\overrightarrow{C{C_1}},\overrightarrow n>=\frac{{3\sqrt{5}}}{2}$,
∴二面角C1-DE-C的正切值为$\frac{{3\sqrt{5}}}{2}$;
(Ⅲ)假设侧棱BB1上是否存在点P,使得CP⊥平面C1DE,设P(2,2,t),则$\overrightarrow{CP}=(2,0,t)$,且$\overrightarrow{CP}$与$\overrightarrow n$共线,
∴存在实数λ使得$\overrightarrow{CP}=λ\overrightarrow n$,即$\left\{\begin{array}{l}2=6λ\\ 0=-3λ\\ t=2λ\end{array}\right.⇒$这样的λ不存在,
∴在侧棱BB1上不存在点P,使得CP⊥平面C1DE.
点评 本题考查直线与平面垂直的判定定理的应用,二面角的平面镜的求法,直线与平面平行的判定定理的应用,考查空间想象能力以及计算能力.


科目:高中数学 来源: 题型:选择题
 如图是表示一个正方体表面的一种平面展开图,图中的四条线段AB、CD、EF和GH在原正方体中不相交的线段的对数为( )
如图是表示一个正方体表面的一种平面展开图,图中的四条线段AB、CD、EF和GH在原正方体中不相交的线段的对数为( )| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
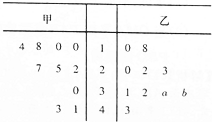 某厂商调查甲乙两种不同型号汽车在10个不同地区卖场的销售量(单位:台),并根据这10个卖场的销售情况,得到如图所示的茎叶图,为了鼓励卖场,在同型号汽车的销售中,该厂商将销售量高于数据平均数的卖场命名为该型号的“星级卖场”
某厂商调查甲乙两种不同型号汽车在10个不同地区卖场的销售量(单位:台),并根据这10个卖场的销售情况,得到如图所示的茎叶图,为了鼓励卖场,在同型号汽车的销售中,该厂商将销售量高于数据平均数的卖场命名为该型号的“星级卖场”查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{π}{6}$ | B. | $\frac{π}{4}$ | C. | $\frac{π}{3}$ | D. | $\frac{π}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3 | B. | 2 | C. | 1 | D. | 0 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com