
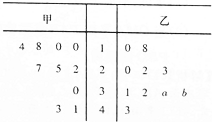
 某厂商调查甲乙两种不同型号汽车在10个不同地区卖场的销售量(单位:台),并根据这10个卖场的销售情况,得到如图所示的茎叶图,为了鼓励卖场,在同型号汽车的销售中,该厂商将销售量高于数据平均数的卖场命名为该型号的“星级卖场”
某厂商调查甲乙两种不同型号汽车在10个不同地区卖场的销售量(单位:台),并根据这10个卖场的销售情况,得到如图所示的茎叶图,为了鼓励卖场,在同型号汽车的销售中,该厂商将销售量高于数据平均数的卖场命名为该型号的“星级卖场”分析 (1)根据茎叶图得到甲组数据的平均值,由此能求出在这10个卖场中,甲型号汽车的“星级卖场”的个数.
(2)记事件A为“a<b”,求出乙组数据的平均值,由此利用列举法能求出a<b的概率.
(3)由方差的性质能求出b=0时,S2达到最小值.
解答 解:(1)根据茎叶图得到甲组数据的平均值:
$\overline{{x}_{甲}}$=$\frac{1}{10}$(10+10+18+14+22+25+27+30+41+43)=24.
∵该厂商将销售量高于数据平均数的卖场命名为该型号的“星级卖场”,
∴在这10个卖场中,甲型号汽车的“星级卖场”的个数为5个.
(2)记事件A为“a<b”,
乙组数据的平均值:
$\overline{{x}_{乙}}$=$\frac{1}{10}$(10+18+20+22+23+31+32+a+a+30+30+43)=26.7,
∴a+b=8,
和取值共9种,分别为:
(0,8),(1,7),(2,6),(3,5),(4,4),(5,3),(6,2),(7,1),(8,0),
其中a<b的有4种,
∴a<b的概率P(A)=$\frac{4}{9}$.
(3)b=0时,S2达到最小值.
点评 本题考查平均数的应用,考查概率和方差的求法,是中档题,解题时要认真审题,注意茎叶图性质的合理运用.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:选择题
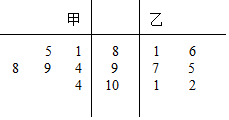 如图是甲、乙两名射击运动员射击6次后所得到的成绩的茎叶图(茎表示成绩的整数环数,叶表示小数点后的数字),由图可知( )
如图是甲、乙两名射击运动员射击6次后所得到的成绩的茎叶图(茎表示成绩的整数环数,叶表示小数点后的数字),由图可知( )| A. | 甲、乙的中位数相等,甲、乙的平均成绩相等 | |
| B. | 甲的中位数比乙的中位数大,乙的平均成绩好 | |
| C. | 甲、乙的中位数相等,乙的平均成绩好 | |
| D. | 甲的中位数比乙的中位数大,甲、乙的平均成绩相等 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{13}{36}$ | B. | $\frac{12}{25}$ | C. | $\frac{13}{25}$ | D. | $\frac{1}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
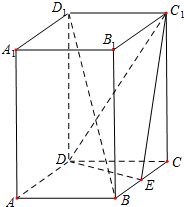 如图,在直四棱柱ABCD-A1B1C1D1中,侧棱AA1的长为3,底面ABCD是边长为2的正方形,E是棱BC的中点.
如图,在直四棱柱ABCD-A1B1C1D1中,侧棱AA1的长为3,底面ABCD是边长为2的正方形,E是棱BC的中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
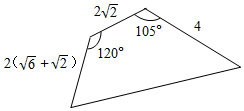 一块四边形土地的形状如图,它的三边长分别是2($\sqrt{6}$+$\sqrt{2}$)m,2$\sqrt{2}$m,4m,两个内角是120°和105°,则四边形的面积为( )
一块四边形土地的形状如图,它的三边长分别是2($\sqrt{6}$+$\sqrt{2}$)m,2$\sqrt{2}$m,4m,两个内角是120°和105°,则四边形的面积为( )| A. | 10+8$\sqrt{3}$m2 | B. | 12+10$\sqrt{3}$m2 | C. | 12+8$\sqrt{3}$m2 | D. | 10+10$\sqrt{3}$m2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com