练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    16．设f（x）为定义在R上的奇函数，当x＞0时，f（x）=2x+1；则f（-2）=-5．

    分析 由题意可得f（-2）=-f（2），计算求得结果．

    解答 解：f（x）为定义在R上的奇函数，当x＞0时，f（x）=2x+1，
    则f（-2）=-f（2）=-（22+1）=-5，
    故答案为：-5．

    点评 本题主要考查利用函数的奇偶性求函数的值，属于基础题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：填空题

    6．给出下列五种说法：
    ①函数$y={x^{\frac{1}{2}}}$与函数$y={（\frac{1}{2}）^x}$的值域相同；
    ②若函数f（x）的定义域为[0，2]，则函数f（2x）的定义域为[0，4]；
    ③函数y=$\frac{1}{2}$+$\frac{1}{{2}^{x}-1}$与$y=\frac{{{{（1+{2^x}）}^2}}}{{x•{2^x}}}$均为奇函数；
    ④若f（x+y）=f（x）f（y），且f（1）=2，$\frac{f（2）}{f（1）}$+$\frac{f（4）}{f（3）}$+…+$\frac{f（2014）}{f（2013）}$+$\frac{f（2016）}{f（2015）}$=2016；
    ⑤已知f（x）=kx，g（x）=（k2-2）x2-2kx，若f（x），g（x）至少有一个在（1，+∞）上单调递增，则实数k的取值范围是$[-\sqrt{3}，-\sqrt{2}）∪（0，+∞）$．
    其中错误说法的序号是①②⑤．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    7．如图是表示一个正方体表面的一种平面展开图，图中的四条线段AB、CD、EF和GH在原正方体中不相交的线段的对数为（　　）
    A．2B．3C．4D．5

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    4．lg1000的值等于（　　）
    A．3B．-3C．0D．1

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    11．对于任意向量$\overrightarrow a$、$\overrightarrow b$、$\overrightarrow c$，下列命题中正确的是（　　）
    A．$|{\overrightarrow a•\overrightarrow b}|=|{\overrightarrow a}||{\overrightarrow b}|$B．$|{\overrightarrow a+\overrightarrow b}|=|{\overrightarrow a}|+|{\overrightarrow b}|$C．$（\overrightarrow a•\overrightarrow b）\overrightarrow c=\overrightarrow a（\overrightarrow b•\overrightarrow c）$D．$\overrightarrow a•\overrightarrow a={|{\overrightarrow a}|^2}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    1．已知函数f（x）=$\frac{a•{2}^{x}+a-2}{{2}^{x}+1}$，（x∈R）是奇函数．
    （1）求实数a的值；
    （2）求证：函数f（x）在R上是单调递增函数；
    （3）求使f（1-m）+f（1-2m）＜0成立的实数m的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    8．sin315°-cos135°+2sin570°=-1．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

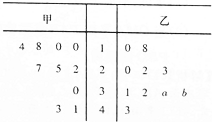    5．某厂商调查甲乙两种不同型号汽车在10个不同地区卖场的销售量（单位：台），并根据这10个卖场的销售情况，得到如图所示的茎叶图，为了鼓励卖场，在同型号汽车的销售中，该厂商将销售量高于数据平均数的卖场命名为该型号的“星级卖场”
    （1）求在这10个卖场中，甲型号汽车的“星级卖场”的个数；
    （2）若在这10个卖场中，乙型号汽车销售量的平均数为26.7，求a＜b的概率；
    （3）若a=1，记乙型号汽车销售量的方差为s2，根据茎叶图推断b为何值时，s2达到最小值（只写出结论）
    注：方差${s^2}=\frac{1}{n}[（{x_1}-\overline x）+（{x_2}-\overline x）+…+（{x_n}-\overline x）]$其中$\overline x$为x1，x2，…，xn的平均数．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    6．求函数f（x）=x（1-x2）在[0，1]上的最大值．

    查看答案和解析>>

    同步练习册答案