
分析 ①根据幂函数和指数函数的性质进行求解即可.
②根据复合函数定义域之间的关系进行求解判断.
③根据函数奇偶性的定义先求出函数的定义域,结合函数奇偶性的定义进行证明.
④利用赋值法进行求解即可.
⑤根据函数单调性的分别进行求解,取并集即可.
解答 解:①函数$y={x^{\frac{1}{2}}}$=$\sqrt{x}$≥0,函数$y={(\frac{1}{2})^x}$>0,则两个函数的值域不相同;故①错误,
②若函数f(x)的定义域为[0,2],则0≤x≤2,
由0≤2x≤2,得0≤x≤1,
即函数f(2x)的定义域为[0,1];故②错误,
③函数y=$\frac{1}{2}$+$\frac{1}{{2}^{x}-1}$=$\frac{{2}^{x}+1}{2({2}^{x}-1)}$,
由2x-1≠0得x≠0,函数的定义域为(-∞,0)∪(0,+∞),
则f(-x)=$\frac{{2}^{-x}+1}{2({2}^{-x}-1)}$=$\frac{1+{2}^{x}}{2(1-{2}^{x})}$=-$\frac{{2}^{x}+1}{2({2}^{x}-1)}$=-f(x),则函数为奇函数,
$y=\frac{{{{(1+{2^x})}^2}}}{{x•{2^x}}}$=$\frac{1+2•{2}^{x}+{4}^{x}}{x•{2}^{x}}$的定义域为(-∞,0)∪(0,+∞),
则f(-x)=$\frac{1+2•{2}^{-x}+{4}^{-x}}{-x•{2}^{-x}}$=$\frac{{4}^{x}+2•{2}^{x}+1}{-x•{2}^{x}}$=-f(x),
则两个函数都是为奇函数;故③正确,
④若f(x+y)=f(x)f(y),且f(1)=2,
令y=1,则f(x+1)=f(x)f(1)=2f(x),
即$\frac{f(x+1)}{f(x)}$=2,
则$\frac{f(2)}{f(1)}$+$\frac{f(4)}{f(3)}$+…+$\frac{f(2014)}{f(2013)}$+$\frac{f(2016)}{f(2015)}$=2×1008=2016;故④正确,
⑤已知f(x)=kx,g(x)=(k2-2)x2-2kx,若f(x)在(1,+∞)上单调递增,
则k>0,
对于g(x)=(k2-2)x2-2kx,
函数的导数g′(x)=2(k2-2)x-2k,
若函数g(x)在(1,+∞)上单调递增,
则g′(x)=2(k2-2)x-2k≥0在(1,+∞)上恒成立,
则$\left\{\begin{array}{l}{2({k}^{2}-2)>0}\\{g'(1)=2({k}^{2}-2)-2k=2({k}^{2}-k-2)≥0}\end{array}\right.$,
即$\left\{\begin{array}{l}{k>\sqrt{2}或k<-\sqrt{2}}\\{k>2或k<-1}\end{array}\right.$,即k>2或k<-$\sqrt{2}$,
若f(x),g(x)至少有一个在(1,+∞)上单调递增,
则k>0或k<-$\sqrt{2}$,
故⑤错误,
故答案为:①②⑤
点评 本题主要考查命题的真假判断,涉及的知识点较多,综合性较强,有一定的难度.


科目:高中数学 来源: 题型:选择题
| A. | -1 | B. | 0 | C. | 1 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 0 | $\frac{π}{2}$ | π | $\frac{3}{2}π$ | |||
| x | 0 | π | ||||
| f(x) |

查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {a|0<a<3} | B. | {a|0≤a<3} | C. | {a|0<a≤3} | D. | {a|0≤a≤3} |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
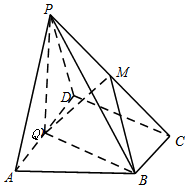 如图,在四棱锥P-ABCD中,底面ABCD为直角梯形,AD∥BC,∠ADC=90°,平面PAD⊥底面ABCD,Q为AD的中点,M是棱PC上的点,PA=PD=2,BC=$\frac{1}{2}$AD=1,CD=$\sqrt{3}$.
如图,在四棱锥P-ABCD中,底面ABCD为直角梯形,AD∥BC,∠ADC=90°,平面PAD⊥底面ABCD,Q为AD的中点,M是棱PC上的点,PA=PD=2,BC=$\frac{1}{2}$AD=1,CD=$\sqrt{3}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
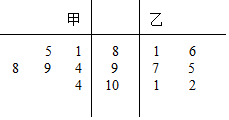 如图是甲、乙两名射击运动员射击6次后所得到的成绩的茎叶图(茎表示成绩的整数环数,叶表示小数点后的数字),由图可知( )
如图是甲、乙两名射击运动员射击6次后所得到的成绩的茎叶图(茎表示成绩的整数环数,叶表示小数点后的数字),由图可知( )| A. | 甲、乙的中位数相等,甲、乙的平均成绩相等 | |
| B. | 甲的中位数比乙的中位数大,乙的平均成绩好 | |
| C. | 甲、乙的中位数相等,乙的平均成绩好 | |
| D. | 甲的中位数比乙的中位数大,甲、乙的平均成绩相等 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com