
分析 求出两个式子的平方,根据平方的结果比较即可.
解答 解:∵($\sqrt{3}$+$\sqrt{5}$)2=3+5+2 $\sqrt{15}$=8+2 $\sqrt{15}$,($\sqrt{2}$+$\sqrt{6}$)2=2+6+2 $\sqrt{12}$=8+2 $\sqrt{12}$,
又∵$\sqrt{12}$<$\sqrt{15}$,$\sqrt{2}$+$\sqrt{6}$>0,$\sqrt{3}$+$\sqrt{5}$>0,
∴$\sqrt{2}+\sqrt{6}$<$\sqrt{3}$+$\sqrt{5}$,
故答案为:>.
点评 本题考查了实数的大小比较的应用,关键是考查学生能否选择适当的方法比较两个实数的大小,如有平方法、倒数法,分析法与综合法等.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
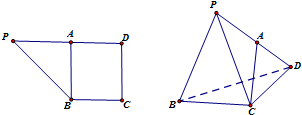 如图,矩形ABCD和直角三角形ABP有共同的边AB,且PA=AD=3,DC=4,沿BD把平面DBP折起,使AC=$\sqrt{7}$.
如图,矩形ABCD和直角三角形ABP有共同的边AB,且PA=AD=3,DC=4,沿BD把平面DBP折起,使AC=$\sqrt{7}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 任何一个算法一定含有顺序结构 | |
| B. | 一个算法可能同时含有顺序结构、条件结构、循环结构 | |
| C. | 循环结构中一定包含条件结构 | |
| D. | 条件结构中一定包含循环结构 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 如图是表示一个正方体表面的一种平面展开图,图中的四条线段AB、CD、EF和GH在原正方体中不相交的线段的对数为( )
如图是表示一个正方体表面的一种平面展开图,图中的四条线段AB、CD、EF和GH在原正方体中不相交的线段的对数为( )| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com