
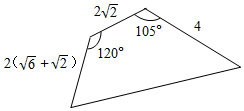
 一块四边形土地的形状如图,它的三边长分别是2($\sqrt{6}$+$\sqrt{2}$)m,2$\sqrt{2}$m,4m,两个内角是120°和105°,则四边形的面积为( )
一块四边形土地的形状如图,它的三边长分别是2($\sqrt{6}$+$\sqrt{2}$)m,2$\sqrt{2}$m,4m,两个内角是120°和105°,则四边形的面积为( )| A. | 10+8$\sqrt{3}$m2 | B. | 12+10$\sqrt{3}$m2 | C. | 12+8$\sqrt{3}$m2 | D. | 10+10$\sqrt{3}$m2 |
分析 通过余弦定理求出其中一条对角线长度,将四边形分成两个三角形,再用S=$\frac{1}{2}$absinC进行解答.
解答  解:如图,连接BD.
解:如图,连接BD.
在△ABD中,由余弦定理得到:BD2=(2$\sqrt{2}$)2+42-2×2$\sqrt{2}$×4cos105°=24-16$\sqrt{2}$(cos60°cos45°-sin60°sin45°)=24-16$\sqrt{2}$×$\frac{\sqrt{2}-\sqrt{6}}{4}$=16+8$\sqrt{3}$,
则BD=2+2$\sqrt{3}$.
在△ABD中,由正弦定理得到:$\frac{BD}{sin105°}$=$\frac{4}{sin∠ABD}$,即$\frac{2+2\sqrt{3}}{\frac{\sqrt{2}+\sqrt{6}}{4}}$=$\frac{4}{sin∠ABD}$,
解得sin∠ABD=$\frac{\sqrt{2}}{2}$.
∴0<∠ABD<120°,
∴∠ABD=45°,
∴∠CBD=120°-45°=75°,
∴S四边形ABCD=S△BCD+S△ABD=$\frac{1}{2}$×4×2$\sqrt{2}$sin105°+$\frac{1}{2}$×2($\sqrt{6}$+$\sqrt{2}$)×(2+2$\sqrt{3}$)sin75°=4$\sqrt{2}$×$\frac{\sqrt{2}+\sqrt{6}}{4}$+($\sqrt{6}$+$\sqrt{2}$)×(2+2$\sqrt{3}$)×$\frac{\sqrt{2}+\sqrt{6}}{4}$=12+8$\sqrt{3}$m2.
故选:C.
点评 本题考查了特殊角的三角函数值,诱导公式,三角函数在直角三角形中的应用,本题中求DB的长度和∠ABD的度数是解题的关键.


 举一反三单元同步过关卷系列答案
举一反三单元同步过关卷系列答案科目:高中数学 来源: 题型:解答题
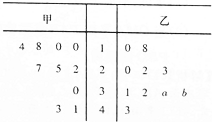 某厂商调查甲乙两种不同型号汽车在10个不同地区卖场的销售量(单位:台),并根据这10个卖场的销售情况,得到如图所示的茎叶图,为了鼓励卖场,在同型号汽车的销售中,该厂商将销售量高于数据平均数的卖场命名为该型号的“星级卖场”
某厂商调查甲乙两种不同型号汽车在10个不同地区卖场的销售量(单位:台),并根据这10个卖场的销售情况,得到如图所示的茎叶图,为了鼓励卖场,在同型号汽车的销售中,该厂商将销售量高于数据平均数的卖场命名为该型号的“星级卖场”查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{π}{6}$ | B. | $\frac{π}{4}$ | C. | $\frac{π}{3}$ | D. | $\frac{π}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3 | B. | 2 | C. | 1 | D. | 0 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com