
分析 写出分段函数解析式,画出图形,把a的最小值转化为求线段MN的最大值,然后利用基本不等式求解.
解答 解:f(x)=(x+1)|x|-3x=$\left\{\begin{array}{l}{{x}^{2}-2x,x≥0}\\{-{x}^{2}-4x,x<0}\end{array}\right.$,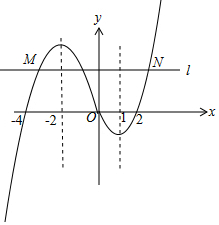
作出分段函数图象如图:
作平行于x轴的直线l与f(x)有3个交点,
设最左边的点为M,最右边的点为N,则a的最小值为线段MN长度的最大值,
设直线l:y=t,则
MN=3+$\sqrt{1+t}+\sqrt{4-t}$=$3+\sqrt{(\sqrt{1+t}+\sqrt{4-t})^{2}}$
=3+$\sqrt{5+2\sqrt{(1+t)(4-t)}}$$≤3+\sqrt{5+1+t+4-t}=3+\sqrt{10}$.
当且仅当1+t=4-t,即t=$\frac{3}{2}$是上式取“=”.
故答案为:$3+\sqrt{10}$.
点评 本题考查恒成立问题,考查数学转化思想方法,解答此题的难点在于把a的最小值转化为求线段MN的最大值,属难题.


科目:高中数学 来源: 题型:选择题
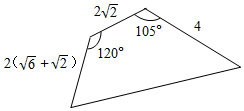 一块四边形土地的形状如图,它的三边长分别是2($\sqrt{6}$+$\sqrt{2}$)m,2$\sqrt{2}$m,4m,两个内角是120°和105°,则四边形的面积为( )
一块四边形土地的形状如图,它的三边长分别是2($\sqrt{6}$+$\sqrt{2}$)m,2$\sqrt{2}$m,4m,两个内角是120°和105°,则四边形的面积为( )| A. | 10+8$\sqrt{3}$m2 | B. | 12+10$\sqrt{3}$m2 | C. | 12+8$\sqrt{3}$m2 | D. | 10+10$\sqrt{3}$m2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 一椭圆和一双曲线的离心率 | B. | 两抛物线的离心率 | ||
| C. | 一椭圆和一抛物线的离心率 | D. | 两椭圆的离心率 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {1,2,3,4,5} | B. | {3} | C. | {1,2,4,5} | D. | {1,5} |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com