
【题目】已知点A(0,3),B(-1,0),C(3,0),求点D的坐标,使四边形ABCD为直角梯形(A,B,C,D按逆时针方向排列).
【答案】见解析
【解析】设所求点D的坐标为(x,y),边AB,BC,CD,AD所在直线的斜率分别为kAB,kBC,kCD,kAD,由于kAB=3,kBC=0,∴kAB·kBC=0≠-1,即AB与BC不垂直,故AB,BC都不可能作为直角梯形的直角边.
(1)若CD是直角梯形的直角边,如图所示,
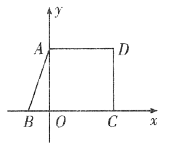
则BC⊥CD,AD⊥CD,
∵kBC=0,∴CD的斜率不存在,从而有x=3.
又∵kAD=kBC,∴![]() ,即y=3,此时AB与CD不平行,故所求点D的坐标为(3,3).
,即y=3,此时AB与CD不平行,故所求点D的坐标为(3,3).
(2)若AD是直角梯形的直角边,如图所示,则AD⊥AB,AD⊥CD,
∵![]() ,∴
,∴![]() ,
,
解得![]() ,故D点坐标为
,故D点坐标为![]() .
.
综上(1)(2)可知,D点坐标为(3,3)或![]() .
.



科目:高中数学 来源: 题型:
【题目】已知二次函数![]() 的图象经过点
的图象经过点![]() ,且函数
,且函数![]() =
= ![]() 是偶函数
是偶函数
(1)求![]() 的解析式;
的解析式;
(2)已知![]() ,求函数
,求函数![]() 在
在![]() 的最大值和最小值
的最大值和最小值
(3)函数![]() 的图象上是否存在这样的点,其横坐标是正整数,纵坐标是一个完全平方数?如果存在,求出这样的点的坐标;如果不存在,请说明理由.
的图象上是否存在这样的点,其横坐标是正整数,纵坐标是一个完全平方数?如果存在,求出这样的点的坐标;如果不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,在三棱柱ABC-A1B1C1中,△ABC与△A1B1C1都为正三角形且AA1⊥面ABC,F、F1分别是AC,A1C1的中点.

求证:(1)平面AB1F1∥平面C1BF;
(2)平面AB1F1⊥平面ACC1A1.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P ABCD中,AB∥CD,AB⊥AD,CD=2AB,平面PAD⊥底面ABCD,PA⊥AD,E和F分别为CD和PC的中点.

求证:(1) BE∥平面PAD;
(2) 平面BEF⊥平面PCD.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知f(x)=logax(a>0且a≠1)的图象过点(4,2),
(1)求a的值.
(2)若g(x)=f(1-x)+f(1+x),求g(x)的解析式及定义域.
(3)在(2)的条件下,求g(x)的单调减区间.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)= ![]() +alnx﹣2,曲线y=f(x)在点P(1,f(1))处的切线与直线y=x+3垂直.
+alnx﹣2,曲线y=f(x)在点P(1,f(1))处的切线与直线y=x+3垂直.
(1)求实数a的值;
(2)记g(x)=f(x)+x﹣b(b∈R),若函数g(x)在区间[e﹣1 , e]上有两个零点,求实数b的取值范围;
(3)若不等式πf(x)>( ![]() )1+x﹣lnx在|t|≤2时恒成立,求实数x的取值范围.
)1+x﹣lnx在|t|≤2时恒成立,求实数x的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】假设某设备的使用年限x(年)和所支出的维修费用y(万元)有如下的统计资料:
x | 2 | 3 | 4 | 5 | 6 |
y | 2.2 | 3.8 | 5.5 | 6.5 | 7.0 |
试求:(1)y与x之间的回归方程;
(2)当使用年限为10年时,估计维修费用是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数 f(x)=2sin2ωx+2sinωxcosωx﹣1(ω>0)的周期为π.
(Ⅰ)求ω的值;
(Ⅱ)求函数f(x)在[ ![]() ,
, ![]() ]上的值域.
]上的值域.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列命题中正确的个数是( )
①若直线l上有无数个点不在平面α内,则l∥α;
②若直线l与平面α平行,则l与平面α内的任意一条直线都平行;
③如果两条平行直线中的一条与一个平面平行,那么另一条也与这个平面平行;
④若直线l与平面α平行,则l与平面α内的任意一条直线都没有公共点.
A.0 B.1
C.2 D.3
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com