
分析 由题意可知,AB=x,即AD=12-x.设PC=a,则DP=x-a,AP=a,再根据△ADP为直角三角形,得出a关于x的表达式,再用三角形面积计算公式,得出△ADP的面积关于x的表达式,再利用基本不等式可得△ADP的面积的最大值及相应的x的值.
解答 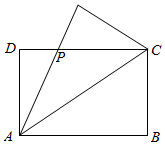 解:由题意可知,矩形ABCD(AB>CD)的周长为24,
解:由题意可知,矩形ABCD(AB>CD)的周长为24,
AB=x,即AD=12-x,
设PC=a,则DP=x-a,AP=a,而△ADP为直角三角形,
∴(12-x)2+(x-a)2=a2,
∴$a=x+\frac{72}{x}-12$,
∴$DP=12-\frac{72}{x}$,
∴${S_{△ADP}}=\frac{1}{2}×AD×DP=\frac{1}{2}×(12-x)×(12-\frac{72}{x})$
=$108-\frac{432}{x}-6x$$≤108-2\sqrt{\frac{432}{x}•6x}$=$108-72\sqrt{2}$.
当且仅当$\frac{432}{x}=6x$时,即$x=6\sqrt{2}$,此时$AD=12-6\sqrt{2}$满足AB>AD,
即$x=6\sqrt{2}$时△ADP取最大面积为$108-72\sqrt{2}$.
点评 本题考查函数的最值的求法,注意运用基本不等式,考查运算能力,属于中档题.


 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案科目:高中数学 来源: 题型:选择题
| A. | (-1,0) | B. | (0,-1) | C. | (1,0) | D. | (0,1) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
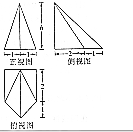 五棱锥P-ABCD的体积为5,三视图如图所示,则侧棱中最长的一条的长度是( )
五棱锥P-ABCD的体积为5,三视图如图所示,则侧棱中最长的一条的长度是( )| A. | 6 | B. | 3$\sqrt{3}$ | C. | 3$\sqrt{2}$ | D. | 4$\sqrt{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
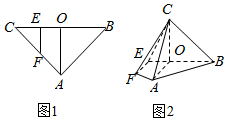 在等腰直角三角形ABC中(图1),斜边BC=6,O为BC的中点,E,F分别在OC和AC上,且EF∥AO,现将三角形以EF为折痕,向上折成60°的二面角,且使C在平面ABEF内的射影恰好为O点(图2)
在等腰直角三角形ABC中(图1),斜边BC=6,O为BC的中点,E,F分别在OC和AC上,且EF∥AO,现将三角形以EF为折痕,向上折成60°的二面角,且使C在平面ABEF内的射影恰好为O点(图2)查看答案和解析>>
科目:高中数学 来源: 题型:选择题
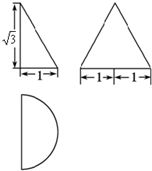
| A. | $\frac{\sqrt{3}π}{2}$+3 | B. | $\frac{3π}{2}$ | C. | π+$\sqrt{3}$ | D. | $\frac{3π}{2}$+$\sqrt{3}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com