
分析 ①对于函数f(x)=sinx,根据其在[-$\frac{π}{2}$,$\frac{π}{2}$]上是单调增函数,通过分析方程sinx=x在[-$\frac{π}{2}$,$\frac{π}{2}$]上仅有一解,判断即可;
②通过对已知函数求导,分析出函数的单调区间,找到极大值点和极小值点,并求出极大值b和极小值a,而求得的f(a)与f(b)在[a,b]范围内,满足性质P;
③根据“性质P”的定义,函数存在“区间M”,只要举出一个符合定义的区间M即可,但要说明函数没有“区间P”,判断即可
解答 解:①对于函数f(x)=sinx,若正弦函数存在等值区间[a,b],
则在区间[a,b]上有sina=a,sinb=b,
由正弦函数的值域知道[a,b]⊆[-1,1],
但在区间]⊆[-1,1]上仅有sin0=0,
所以函数f(x)=sinx不具有性质P;
②对于函数f(x)=x3-3x,f′(x)=3x2-3=3(x-1)(x+1).
当x∈(-1,1)时,f′(x)0.
所以函数f(x)=x3-3x的增区间是(-∞,-1),(1,+∞),减区间是(-1,1).
取M=[-2,2],此时f(-2)=-2,f(-1)=2,f(1)=-2,f(2)=2.
所以函数f(x)=x3-3x在M=[-2,2]上的值域也为[-2,2],
则具有性质P;
③对于 f(x)=lgx+3,若存在“稳定区间”[a,b],由于函数是定义域内的增函数,
故有$\left\{\begin{array}{l}lga+3=a\\ lgb+3=b\end{array}\right.$,即方程lgx+3=x有两个解,这与y=lgx+3和y=x的图象相切相矛盾.
故③不具有性质P.
故答案为:②.
点评 本题是新定义题,考查了函数的定义域与值域的关系,体现了数学转化思想,此题中单调函数存在好区间的条件是f(x)=x,正确理解“性质P”的定义是解答该题的关键,是中档题


科目:高中数学 来源: 题型:解答题
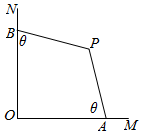 某菜农有两段总长度为20米的篱笆PA及PB,现打算用它们和两面成直角的墙OM、ON围成一个如图所示的四边形菜园OAPB(假设OM、ON这两面墙都足够长).已知|PA|=|PB|=10(米),∠AOP=∠BOP=$\frac{π}{4}$,∠OAP=∠OBP.设∠OAP=θ,四边形OAPB的面积为S.
某菜农有两段总长度为20米的篱笆PA及PB,现打算用它们和两面成直角的墙OM、ON围成一个如图所示的四边形菜园OAPB(假设OM、ON这两面墙都足够长).已知|PA|=|PB|=10(米),∠AOP=∠BOP=$\frac{π}{4}$,∠OAP=∠OBP.设∠OAP=θ,四边形OAPB的面积为S.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{2}$ | B. | $\sqrt{3}$ | C. | 2 | D. | 2$+\sqrt{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -$\frac{3\sqrt{3}}{2}$ | B. | -$\frac{2\sqrt{3}}{2}$ | C. | $\frac{2\sqrt{3}}{2}$ | D. | $\frac{3\sqrt{3}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {a|a<-3或a>1} | B. | {a|a>1} | C. | {a|-3<x<1} | D. | {a|a<-3} |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com