
分析 (1)求出f(x)的最小值,得到|a+2|=3,解出a的值即可;
(2)问题转化为|x+a|≤2,求出x的范围,结合集合的包含关系得到关于a的不等式组,解出即可.
解答 解:(1)∵f(x)=|x-2|+|x+a|≥|(x-2)-(x+a)|=|a+2|,
当且仅当(x-2)(x+a)≤0时取等号,
∴f(x)min=|a+2|,
由|a+2|=3,解得:a=1或a=-5;
(2)当x∈[1,2]时,f(x)=|x+a|+2-x=
而|x-4|=-x+4,
由|x-4|≥f(x)恒成立,
得-x+4≥-x+2+|x+a|,
即|x+a|≤2,解得:-2-a≤x≤2-a,
由题意得[1,2]⊆[-2-a,2-a],
则$\left\{\begin{array}{l}{2-a≥2}\\{-2-a≤1}\end{array}\right.$,即-3≤a≤0.
∴a的取值范围[-3,0]
点评 本题考查了解绝对值不等式问题,考查了分类讨论思想,是一道中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
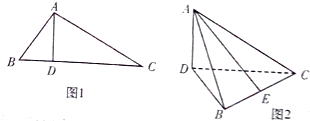 如图1,在Rt△ABC中,∠ABC=60°,∠BAC=90°,AD是BC上的高,沿AD将△ABC折成600的二面角B-AD-C,如图2.
如图1,在Rt△ABC中,∠ABC=60°,∠BAC=90°,AD是BC上的高,沿AD将△ABC折成600的二面角B-AD-C,如图2.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ①和② | B. | ①和③ | C. | ①和④ | D. | ③和④ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com