Question

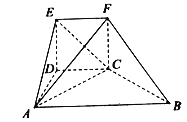
【题目】如图，几何体EF-ABCD中，四边形CDEF是正方形，四边形ABCD为直角梯形，AB∥CD，AD⊥DC，△ACB是腰长为2的等腰直角三角形，平面CDEF⊥平面ABCD．

（1）求证：BC⊥AF；

（2）求几何体EF-ABCD的体积．

Answer 1

【答案】（1）详见解析；（2）.

【解析】

（1）推导出FC⊥CD，FC⊥BC，AC⊥BC，由此BC⊥平面ACF，从而BC⊥AF．

（2）推导出AC＝BC＝2，AB4，从而AD＝BCsin∠ABC＝22，由V几何体EF﹣ABCD＝V几何体A﹣CDEF+V几何体F﹣ACB，能求出几何体EF﹣ABCD的体积．

（1）因为平面CDEF⊥平面ABCD，

平面CDEF∩平面ABCD=CD，

又四边形CDEF是正方形，

所以FC⊥CD，FC平面CDEF，

所以FC⊥平面ABCD，所以FC⊥BC．

因为△ACB是腰长为2的等腰直角三角形，

所以AC⊥BC．

又AC∩CF=C，所以BC⊥平面ACF．

所以BC⊥AF．

（2）因为△ABC是腰长为2的等腰直角三角形，

所以AC=BC=2，AB==4，

所以AD=BCsin∠ABC=2=2，

CD=AB=BCcos∠ABC=4-2cos45°=2，

∴DE=EF=CF=2，

由勾股定理得AE==2，

因为DE⊥平面ABCD，所以DE⊥AD．

又AD⊥DC，DE∩DC=D，所以AD⊥平面CDEF．

所以V几何体EF-ABCD=V几何体A-CDEF+V几何体F-ACB

=

=+

=

=．