
分析 (Ⅰ)利用已知条件推出f(a)≥f(-b),f(b)≥f(-a) 然后推出f(a)+f(b)≥f(-a)+f(-b).
(Ⅱ)写出逆命题,判断该命题是真命题,用反证法证明:假设a+b<0,则a<-b,b<-a,推出f(a)+f(b)<f(-a)+f(-b)与已知f(a)+f(b)≥f(-a)+f(-b)矛盾,得到结果.
解答 (本小题满分12分)
解:(Ⅰ)因为a+b≥0,∴a≥-b,
又函数f(x)是R上的增函数,∴f(a)≥f(-b)…(2分)
同理f(b)≥f(-a) …(3分)
所以f(a)+f(b)≥f(-a)+f(-b) …(5分)
(Ⅱ)逆命题是:
“已知函数f(x)是R上的增函数,若f(a)+f(b)≥f(-a)+f(-b),则a+b≥0”…(7分)
该命题是真命题.…(8分)
用反证法证明如下:
假设a+b<0,则a<-b,b<-a,
由函数f(x)是R上的增函数得:f(a)<f(-b),f(b)<f(-a),
∴f(a)+f(b)<f(-a)+f(-b)
…(10分)这与已知f(a)+f(b)≥f(-a)+f(-b)矛盾 …(11分)
所以逆命题为真命题. …(12分)
点评 本题考查函数的单调性的应用,命题的真假的判断与应用,不等式的证明,反证法的应用,考查分析问题解决问题的能力.


 互动课堂系列答案
互动课堂系列答案 激活思维智能训练课时导学练系列答案
激活思维智能训练课时导学练系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
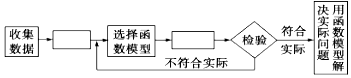
| A. | 整理数据、求函数关系式 | B. | 画散点图、进行模型修改 | ||
| C. | 画散点图、求函数关系式 | D. | 整理数据、进行模型修改 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 某少数民族的刺绣有着悠久的历史,如图①②③④是刺绣中最简单的四个图案,这些图案都是由小正方形构成的,小正方形的个数越多刺绣越漂亮.现按同样的规律刺绣,设第n个图案包含f(n)个小正方形.
某少数民族的刺绣有着悠久的历史,如图①②③④是刺绣中最简单的四个图案,这些图案都是由小正方形构成的,小正方形的个数越多刺绣越漂亮.现按同样的规律刺绣,设第n个图案包含f(n)个小正方形.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com