
 某少数民族的刺绣有着悠久的历史,如图①②③④是刺绣中最简单的四个图案,这些图案都是由小正方形构成的,小正方形的个数越多刺绣越漂亮.现按同样的规律刺绣,设第n个图案包含f(n)个小正方形.
某少数民族的刺绣有着悠久的历史,如图①②③④是刺绣中最简单的四个图案,这些图案都是由小正方形构成的,小正方形的个数越多刺绣越漂亮.现按同样的规律刺绣,设第n个图案包含f(n)个小正方形.分析 (1)先分别观察给出正方体的个数为:1,1+4,1+4+8,…从而得出f(5);
(2)将(1)总结一般性的规律:f(n+1)与f(n)的关系式,再从总结出来的一般性的规律转化为特殊的数列再求解即得
解答 解:(1)∵f(1)=1,f(2)=5,f(3)=13,f(4)=25,
∴f(2)-f(1)=4=4×1.
f(3)-f(2)=8=4×2,
f(4)-f(3)=12=4×3,
f(5)-f(4)=16=4×4
∴f(5)=25+4×4=41.
(2)由上式规律得出f(n+1)-f(n)=4n.
∴f(2)-f(1)=4×1,
f(3)-f(2)=4×2,
f(4)-f(3)=4×3,
…
f(n-1)-f(n-2)=4•(n-2),
f(n)-f(n-1)=4•(n-1)
∴f(n)-f(1)=4[1+2+…+(n-2)+(n-1)]=2(n-1)•n,
∴f(n)=2n2-2n+1.
点评 本题主要考查归纳推理,其基本思路是先分析具体,观察,总结其内在联系,得到一般性的结论,若求解的项数较少,可一直推理出结果,若项数较多,则要得到一般求解方法,再求具体问题.


 孟建平名校考卷系列答案
孟建平名校考卷系列答案科目:高中数学 来源: 题型:选择题
| A. | $\frac{\sqrt{2}}{5}$ | B. | 2$\sqrt{2}$ | C. | $\sqrt{2}$ | D. | $\frac{\sqrt{2}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
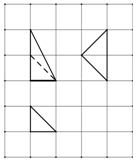 某几何体的三视图如图所示,网格纸的小方格是边长为1的正方形,则该几何体中最长的棱长是( )
某几何体的三视图如图所示,网格纸的小方格是边长为1的正方形,则该几何体中最长的棱长是( )| A. | $\sqrt{5}$ | B. | $\sqrt{6}$ | C. | $\sqrt{7}$ | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 70 | B. | 68 | C. | 69 | D. | 71 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
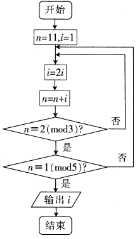 《孙子算经》是中国公元四世纪的数学著作,其中接受了求解依次同余式的方法,他是数论中一个重要的定理,又称《中国剩余定理》,如图所示的程序框图的算法就是源于《中国剩余定理》,执行该程序框图,若正整数N除以正整数m后的余数为n,则记为N≡n(modm),例如11≡3(mod4),则输出的等于( )
《孙子算经》是中国公元四世纪的数学著作,其中接受了求解依次同余式的方法,他是数论中一个重要的定理,又称《中国剩余定理》,如图所示的程序框图的算法就是源于《中国剩余定理》,执行该程序框图,若正整数N除以正整数m后的余数为n,则记为N≡n(modm),例如11≡3(mod4),则输出的等于( )| A. | 8 | B. | 16 | C. | 32 | D. | 64 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com