
分析 (1)利用已知条件转化求解数列{an+4}是等比数列,然后求出{an}通项公式.
(2)化简数列通项公式bn,利用错位相减法求和求解即可.
解答 解:(1)证明:∵a1=-2,∴a1+4=2,
∵an+1=2an+4,∴an+1+4=2an+8=2(an+4),
∴$\frac{{{a_{n+1}}+4}}{{{a_n}+4}}=2$,
∴{an+4}是以2为首项,2为公比的等比数列,
由上知${a_n}+4={2^n}$,∴${a_n}={2^n}-4$.…(4分)
(2)${b_n}=({a_n}+4)•{log_{\frac{1}{2}}}({a_{n+1}}+4)={2^n}•(-1)•{log_2}({2^{n+1}})=-(n+1)•{2^n}$
∴${S_n}=-[2×{2^1}+3×{2^2}+4×{2^3}+…+(n+1)×{2^n}]$,①
$2{S_n}=-[2×{2^2}+3×{2^3}+4×{2^4}+…+(n+1)×{2^{n+1}}]$,②
②-①得:${S_n}=2×{2^1}+{2^2}+{2^3}+{2^4}+…+{2^n}-(n+1)×{2^{n+1}}$
=$2+\frac{{2×(1-{2^n})}}{1-2}-(n+1)×{2^{n+1}}$
=2+2n+1-2-(n+1)×2n+1
=-n•2n+1.…(8分)
点评 本题考查数列的递推关系式的应用,数列求和的方法,考查转化思想以及计算能力.


科目:高中数学 来源: 题型:选择题
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分又不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 某少数民族的刺绣有着悠久的历史,如图①②③④是刺绣中最简单的四个图案,这些图案都是由小正方形构成的,小正方形的个数越多刺绣越漂亮.现按同样的规律刺绣,设第n个图案包含f(n)个小正方形.
某少数民族的刺绣有着悠久的历史,如图①②③④是刺绣中最简单的四个图案,这些图案都是由小正方形构成的,小正方形的个数越多刺绣越漂亮.现按同样的规律刺绣,设第n个图案包含f(n)个小正方形.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
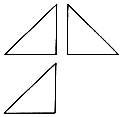 在体积为V的球内有一个多面体,该多面体的三视图是如图所示的三个斜边都是$\sqrt{2}$的等腰直角三角形,则V的最小值是( )
在体积为V的球内有一个多面体,该多面体的三视图是如图所示的三个斜边都是$\sqrt{2}$的等腰直角三角形,则V的最小值是( )| A. | $4\sqrt{3π}$ | B. | $\frac{{\sqrt{3}π}}{2}$ | C. | 3π | D. | 12π |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com