
分析 利用|$\overrightarrow{a}$-$\overrightarrow{b}$|=$\sqrt{(x-1)^{2}+(y-2)^{2}}$≥|$\overrightarrow{OP}$|-1,即可求出
解答 解:设O(0,0),P(1,2),
∴|$\overrightarrow{a}$-$\overrightarrow{b}$|=$\sqrt{(x-1)^{2}+(y-2)^{2}}$≥|$\overrightarrow{OP}$|-1=$\sqrt{{1}^{2}+{2}^{2}}$-1=$\sqrt{5}$-1,
∴|$\overrightarrow{a}$-$\overrightarrow{b}$|的最小值为$\sqrt{5}$-1
点评 本题考查了向量的模的计算公式、点与圆的位置关系,考查了推理能力与计算能力,属于基础题


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
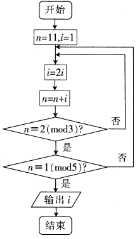 《孙子算经》是中国公元四世纪的数学著作,其中接受了求解依次同余式的方法,他是数论中一个重要的定理,又称《中国剩余定理》,如图所示的程序框图的算法就是源于《中国剩余定理》,执行该程序框图,若正整数N除以正整数m后的余数为n,则记为N≡n(modm),例如11≡3(mod4),则输出的等于( )
《孙子算经》是中国公元四世纪的数学著作,其中接受了求解依次同余式的方法,他是数论中一个重要的定理,又称《中国剩余定理》,如图所示的程序框图的算法就是源于《中国剩余定理》,执行该程序框图,若正整数N除以正整数m后的余数为n,则记为N≡n(modm),例如11≡3(mod4),则输出的等于( )| A. | 8 | B. | 16 | C. | 32 | D. | 64 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{57}$ | B. | $\sqrt{61}$ | C. | 57 | D. | 61 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{x^2}{9}+\frac{y^2}{16}=1$ | B. | $\frac{x^2}{25}+\frac{y^2}{16}=1$ | ||
| C. | $\frac{x^2}{25}+\frac{y^2}{16}=1$或$\frac{x^2}{16}+\frac{y^2}{25}=1$ | D. | $\frac{x^2}{16}+\frac{y^2}{25}=1$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com