
分析 根据二阶矩阵与平面列向量的乘法,确定矩阵M,再求矩阵的逆矩阵.
解答 解:由题意知,$M[\begin{array}{l}2\\ 2\end{array}]=[\begin{array}{l}-1-\sqrt{3}\\-1+\sqrt{3}\end{array}]$,即$[\begin{array}{l}2cosα-2sinα\\ 2sinα+2cosα\end{array}]=[\begin{array}{l}-1-\sqrt{3}\\-1+\sqrt{3}\end{array}]$----------------------(2分)
所以$\left\{\begin{array}{l}2cosα-2sinα=-1-\sqrt{3}\\ 2sinα+2cosα=-1+\sqrt{3}\end{array}\right.$解得$\left\{\begin{array}{l}cosα=-\frac{1}{2}\\ sinα=\frac{{\sqrt{3}}}{2}\end{array}\right.$从而$M=[\begin{array}{l}-\frac{1}{2}-\frac{{\sqrt{3}}}{2}\\ \frac{{\sqrt{3}}}{2}-\frac{1}{2}\end{array}]$-----------(6分)
由${M^{-1}}M=[\begin{array}{l}1\;\;\;\;\;0\\ 0\;1\end{array}]$,解得${M^{-1}}=[{\begin{array}{l}{-\frac{1}{2}}&{\frac{{\sqrt{3}}}{2}}\\{-\frac{{\sqrt{3}}}{2}}&{-\frac{1}{2}}\end{array}}]$.----------------------------------------(10分)
点评 本题考查矩阵的求法,考查矩阵的逆矩阵,属于基础题.


科目:高中数学 来源: 题型:选择题
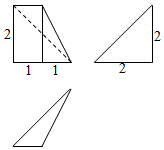
| A. | $\frac{2}{3}$ | B. | $\frac{4}{3}$ | C. | 2 | D. | $\frac{8}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -$\frac{4}{5}$ | B. | -$\frac{3}{5}$ | C. | 0 | D. | $\frac{3}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
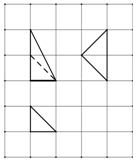 某几何体的三视图如图所示,网格纸的小方格是边长为1的正方形,则该几何体中最长的棱长是( )
某几何体的三视图如图所示,网格纸的小方格是边长为1的正方形,则该几何体中最长的棱长是( )| A. | $\sqrt{5}$ | B. | $\sqrt{6}$ | C. | $\sqrt{7}$ | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题

| A. | $\sqrt{2}$ | B. | $\frac{{\sqrt{2}}}{2}$ | C. | $\frac{{\sqrt{2}}}{3}$ | D. | $\frac{{\sqrt{2}}}{6}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{x^2}{9}+\frac{y^2}{16}=1$ | B. | $\frac{x^2}{25}+\frac{y^2}{16}=1$ | ||
| C. | $\frac{x^2}{25}+\frac{y^2}{16}=1$或$\frac{x^2}{16}+\frac{y^2}{25}=1$ | D. | $\frac{x^2}{16}+\frac{y^2}{25}=1$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com