练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    15．函数f（x）=$\sqrt{-{x^2}+2x+3}$+lg（x2-1）的定义域是（1，3]．

    分析 根据函数成立的条件即可求函数的定义域．

    解答 解：要使函数有意义，则$\left\{\begin{array}{l}{-x^2+2x+3≥0}\\{x^2-1＞0}\end{array}\right.$，
    即$\left\{\begin{array}{l}{x^2-2x-3≤0}\\{x＞1或x＜-1}\end{array}\right.$，
    则$\left\{\begin{array}{l}{-1≤x≤3}\\{x＞1或x＜-1}\end{array}\right.$，
    解得1＜x≤3，
    故定义域为（1，3]，
    故答案为：（1，3]

    点评 本题主要考查函数的定义域的求解，要求熟练掌握常见函数成立的条件．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：选择题

    5．正四面体ABCD中，M，N分别是棱BC和棱AC的中点，则异面直线AM和DN所成的角的余弦值为（　　）
    A．$\frac{1}{2}$B．$\frac{1}{3}$C．$\frac{1}{6}$D．0

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    6．已知抛物线C：y2=2px（p＞0）的焦点为F，点F是双曲线：$\frac{3{x}^{2}}{5}$-$\frac{3{y}^{2}}{7}$=1的一个焦点；
    （1）求抛物线C的方程；
    （2）过点F任作直线l与曲线C交于A，B两点．
    ①求$\overrightarrow{OA}$•$\overrightarrow{OB}$的值；②由点A，B分别向（x-2）2+y2=1各引一条切线切点分别为P、Q，记α=∠AFP，β=∠BFQ，求cosα+cosβ的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

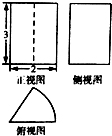    3．某由圆柱切割获得的几何体的三视图如图所示，其中俯视图是中心角为60°的扇形，则该几何体的体积为（　　）
    A．2πB．πC．$\frac{2π}{3}$D．$\frac{π}{3}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    10．一个几何体的三视图如图所示，则该几何体的表面积为（　　）
    A．6πB．7πC．8πD．9π

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    20．七位裁判各自对一名跳水运动员打分后，去掉一个最高分，再去掉一个最低分，关于剩余分数的说法一定正确的是（　　）
    A．众数不变B．方差不变C．平均值不变D．中位数不变

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    7．在三棱柱ABC-A1B1C1中，△ABC为正三角形，AA1⊥底面ABC，E是AB的中点，F是BC1的中点．下列命题正确的是①②③⑤（写出所有正确命题的编号）．
    ①EF∥平面ACC1A1；
    ②平面CEF⊥平面 ABB1A1；
    ③平面CEF截该三棱柱所得大小两部分的体积比为11：1；
    ④若该三棱柱有内切球，则AB=$\sqrt{3}$BB1；
    ⑤若BB1上有唯一点G，使得A1G⊥CG，则BB1=$\sqrt{2}$AB．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    4．已知点A（-2，0），B（0，-2），C（2sinθ，cosθ）．
    （Ⅰ）若|$\overrightarrow{AC}$|=|$\overrightarrow{BC}$|，求tanθ和$\frac{3sinθ-4cosθ}{4cosθ+3sinθ}$的值；
    （Ⅱ）若（$\overrightarrow{OA}$+2$\overrightarrow{OB}$）•$\overrightarrow{OC}$=1，其中O为坐标原点，求sinθ•cosθ的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    5．圆柱形容器盛有为8cm的水，现放入三个相同的玻璃小球（小球的半径与圆柱的底面半径相等），若水刚好淹没最上方的小球，如图所示，则小球的半径为4．

    查看答案和解析>>

    同步练习册答案