
分析 (Ⅰ)当a=1,解不等式f(x)>1,即x2+x-1>1,通过因式分解,即可求解.
(Ⅱ)若a<0,解不等式f(x)>1.通过因式分解,求解f(x)的两个根,讨论根的大小关系可得不等式的解集.
解答 解:(Ⅰ)当a=1时,解不等式f(x)>1,即x2+x-1>1,因式分解得:(x+2)(x-1)>0
解得:x>1或x<-2
故不等式的解集为{x|x>1或x<-2}.
(Ⅱ)若a<0,解不等式f(x)>1.即ax2+ax-1>1,因式分解得:(x+$\frac{a+1}{a}$)(x-1)>0
当a$<-\frac{1}{2}$时,1$>-\frac{a+1}{a}$,此时不等式的解集为{x|$-\frac{a+1}{a}<a<1$};
当a=$-\frac{1}{2}$时,1=$\frac{a+1}{a}$,此时不等式为(x-1)2>0,则不等式的解集为{x∈R|x≠1};
当0>a$>-\frac{1}{2}$时,1$<\frac{a+1}{a}$,此时不等式的解集为{x|$1<x<-\frac{a+1}{a}$};
综上可得:当a$<-\frac{1}{2}$时,不等式的解集为{x|$-\frac{a+1}{a}<a<1$};
当a=$-\frac{1}{2}$时,不等式的解集为{x∈R|x≠1};
当0>a$>-\frac{1}{2}$时,不等式的解集为{x|$1<x<-\frac{a+1}{a}$}.
点评 本题考查了不等式的解法与应用问题,解题时应对字母系数进行分析,是基础题.


 中考解读考点精练系列答案
中考解读考点精练系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
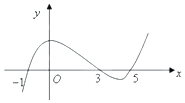
| A. | (-1,3)为函数y=f(x)的递增区间 | B. | (3,5)为函数y=f(x)的递减区间 | ||
| C. | 函数y=f(x)在x=0处取得极大值 | D. | 函数y=f(x)在x=5处取得极小值 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {5} | B. | {0,3} | C. | {0,2,3,5} | D. | ∅ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 已知P(0,-1)是椭圆C的下顶点,F是椭圆C的右焦点,直线PF与椭圆C的另一个交点为Q,满足$\overrightarrow{PF}$=7$\overrightarrow{FQ}$.
已知P(0,-1)是椭圆C的下顶点,F是椭圆C的右焦点,直线PF与椭圆C的另一个交点为Q,满足$\overrightarrow{PF}$=7$\overrightarrow{FQ}$.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com