Question

7．在△ABC中，$∠ABC=\frac{2π}{3}$，过B点作BD⊥AB交AC于点D．若AB=CD=1，则AD=$\root{3}{2}$．

Answer 1

分析 设AD=x，由题意求出∠CBD、sin∠BDC，由正弦定理求出BC，在△ABC中由余弦定理列出方程，化简后求出x的值，可得答案．

解答 解：设AD=x，且BD⊥AB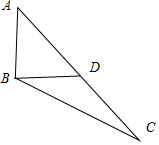，AB=CD=1，
在△BCD中，$∠ABC=\frac{2π}{3}$，则$∠CBD=\frac{π}{6}$，
且sin∠BDC=sin（π-∠ADB）=sin∠ADB=$\frac{AB}{AD}$=$\frac{1}{x}$，
由正弦定理得，$\frac{BC}{sin∠BDC}=\frac{CD}{sin∠CBD}$，
所以BC=$\frac{CD•sin∠BDC}{sin∠CBD}$=$\frac{1×\frac{1}{x}}{\frac{1}{2}}$=$\frac{2}{x}$，
在△ABC中，由余弦定理得，
AC²=AB²+BC²-2•AB•BCcos∠ABC
则${（1+x）}^{2}=1+（\frac{2}{x}）-2×1×\frac{2}{x}×（-\frac{1}{2}）$，化简得，${x}^{2}+2x=\frac{2x+4}{{x}^{2}}$，
解得x=$\root{3}{2}$，即AD=$\root{3}{2}$，
故答案为：$\root{3}{2}$．

点评 本题考查正弦定理，余弦定理的应用，考查方程思想，化简、计算能力．