
【题目】已知椭圆![]() 的左、右焦点分别为
的左、右焦点分别为![]() ,离心率为
,离心率为![]() ,
,![]() 为椭圆上一动点(异于左右顶点),
为椭圆上一动点(异于左右顶点),![]() 面积的最大值为
面积的最大值为![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)若直线![]() 与椭圆
与椭圆![]() 相交于点
相交于点![]() 两点,问
两点,问![]() 轴上是否存在点
轴上是否存在点![]() ,使得
,使得![]() 是以
是以![]() 为直角顶点的等腰直角三角形?若存在,求点
为直角顶点的等腰直角三角形?若存在,求点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
 一线名师提优试卷系列答案
一线名师提优试卷系列答案 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案科目:高中数学 来源: 题型:
【题目】设O为坐标原点,动点M在椭圆C![]() 上,过M作x轴的垂线,垂足为N,点P满足
上,过M作x轴的垂线,垂足为N,点P满足![]() .
.
(1)求点P的轨迹方程;
(2)设点![]() 在直线
在直线![]() 上,且
上,且![]() .证明:过点P且垂直于OQ的直线
.证明:过点P且垂直于OQ的直线![]() 过C的左焦点F.
过C的左焦点F.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
:![]() ,动直线l与椭圆E交于不同的两点
,动直线l与椭圆E交于不同的两点![]() ,
,![]() ,且△AOB的面积为1,其中O为坐标原点.
,且△AOB的面积为1,其中O为坐标原点.
(1)证明:![]() 为定值;
为定值;
(2)设线段AB的中点为M,求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】新型冠状病毒属于![]() 属的冠状病毒,有包膜,颗粒常为多形性,其中包含着结构为数学模型的
属的冠状病毒,有包膜,颗粒常为多形性,其中包含着结构为数学模型的![]() ,
,![]() ,人体肺部结构中包含
,人体肺部结构中包含![]() ,
,![]() 的结构,新型冠状病毒肺炎是由它们复合而成的,表现为
的结构,新型冠状病毒肺炎是由它们复合而成的,表现为![]() .则下列结论正确的是( )
.则下列结论正确的是( )
A.若![]() ,则
,则![]() 为周期函数
为周期函数
B.对于![]() ,
,![]() 的最小值为
的最小值为![]()
C.若![]() 在区间
在区间![]() 上是增函数,则
上是增函数,则![]()
D.若![]() ,
,![]() ,满足
,满足![]() ,则
,则![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)=ex﹣ax+a(a∈R),其图象与x轴交于A(x1,0),B(x2,0)两点,且x1<x2.
(1)求a的取值范围;
(2)证明:f′(![]() )<0(f′(x)为函数f(x)的导函数);
)<0(f′(x)为函数f(x)的导函数);
(3)设点C在函数y=f(x)的图象上,且△ABC为等腰直角三角形,记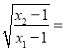 t,求(a﹣1)(t﹣1)的值.
t,求(a﹣1)(t﹣1)的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,
,![]() ,
,![]() .
.
(1)求函数![]() 的单调增区间;
的单调增区间;
(2)令![]() ,且函数
,且函数![]() 有三个彼此不相等的零点0,m,n,其中
有三个彼此不相等的零点0,m,n,其中![]() .
.
①若![]() ,求函数
,求函数![]() 在
在![]() 处的切线方程;
处的切线方程;
②若对![]() ,
,![]() 恒成立,求实数t的去取值范围.
恒成立,求实数t的去取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,左、右焦点分别是
,左、右焦点分别是![]() ,椭圆
,椭圆![]() 上短轴的一个端点与两个焦点构成的三角形的面积为
上短轴的一个端点与两个焦点构成的三角形的面积为![]() ;
;
(1)求椭圆![]() 的方程;
的方程;
(2)过![]() 作垂直于
作垂直于![]() 轴的直线
轴的直线![]() 交椭圆
交椭圆![]() 于
于![]() 两点(点
两点(点![]() 在第二象限),
在第二象限),![]() 是椭圆上位于直线
是椭圆上位于直线![]() 两侧的动点,若
两侧的动点,若![]() ,求证:直线
,求证:直线![]() 的斜率为定值.
的斜率为定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲、乙两名枪手进行射击比赛,每人各射击三次,甲三次射击命中率均为![]() ;乙第一次射击的命中率为
;乙第一次射击的命中率为![]() ,若第一次未射中,则乙进行第二次射击,射击的命中率为
,若第一次未射中,则乙进行第二次射击,射击的命中率为![]() ,如果又未中,则乙进行第三次射击,射击的命中率为
,如果又未中,则乙进行第三次射击,射击的命中率为![]() .乙若射中,则不再继续射击.则甲三次射击命中次数的期望为_____,乙射中的概率为_____.
.乙若射中,则不再继续射击.则甲三次射击命中次数的期望为_____,乙射中的概率为_____.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】众所周知,大型网络游戏(下面简称网游)的运行必须依托于网络的基础上,否则会出现频繁掉线的情况,进而影响游戏的销售和推广,某网游经销在甲地区5个位置对两种类型的网络(包括“电信”和“网通”)在相同条件下进行游戏掉线的测试,得到数据如下:
位置 类型 | A | B | C | D | E |
电信 | 4 | 3 | 8 | 6 | 12 |
网通 | 5 | 7 | 9 | 4 | 3 |
(1)如果在测试中掉线次数超过5次,则网络状况为“糟糕”,否则为“良好”,那么在犯错误的概率不超过0.15的前提下,能否说明网络状况与网络的类型有关?
(2)若该游戏经销商要在上述接受测试的电信的5个地区中任选2个作为游戏推广,求A,B两地区至少选到一个的概率.
参考公式: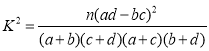 .
.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com